练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
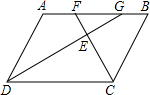
    14．如图，平行四边形ABCD中，∠BCD的平分线CF交AB于点F，∠ADC的平分线DG交边AB于点G．AD=6，DC=8，求证：AF=BG．

    分析 由平行四边形ABCD中，∠BCD的平分线CF交AB于点F，∠ADC的平分线DG交边AB于点G，易证得△ADG与△BCF是等腰三角形，继而证得结论．

    解答 证明：∵四边形ABCD是平行四边形，
    ∴AB∥CD，AD=BC，
    ∴∠AGD=∠CDG，∠BFC=∠DCF，
    ∵∠BCD的平分线CF交AB于点F，∠ADC的平分线DG交边AB于点G，
    ∴∠ADG=∠CDG，∠BCF=∠DCF，
    ∴∠ADG=∠AGD，∠BFC=∠BCF，
    ∴AG=AD，BC=BF，
    ∴AG=BF，
    ∴AF=BG．

    点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质．注意证得△ADG与△BCF是等腰三角形是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．如图，在△ABC中，AB=AC，点D是BC的中点，BF⊥AC于点F，交AD于点E，∠BAC=45°．求证：△AEF≌△BCF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

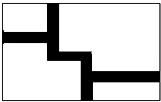    5．如图，在长为32 米，宽为20 米的矩形地面上修建同样宽度的道路（图中阴影部分），余下的部分种植草坪，要使草坪的面积为540m2，求道路的宽是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知下列方程：（1）2x+3=$\frac{4}{x}$；（2）7x=9；（3）4x-2=3x+1；（4）x2+6x+9=0（5）x+y=8．其中是一元一次方程的个数是（　　）
    A．2B．3C．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．在数轴上表示出下列各有理数：-0.7，-3，-2$\frac{1}{3}$，0，1$\frac{1}{2}$，2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）$\sqrt{48}$×$\sqrt{300}$    
    （2）$\sqrt{18}$÷（3$\sqrt{2}$×2$\sqrt{2}$）　    
    （3）$\sqrt{3}$×$\sqrt{2}$÷$\sqrt{30}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各式中正确的是（　　）
    A．（a-b）2=a2-b2B．（a+2b）2=a2+2ab+b2C．（a+b）2=a2+b2D．（-a+b）2=a2-2ab+b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）（-99$\frac{15}{16}$）×8；
    （2）（-11）×（-$\frac{2}{5}$）+（-11）×（+2$\frac{3}{5}$）+（-11）×（-$\frac{1}{5}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

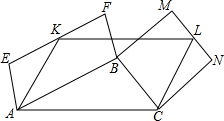    4．在△ABC的边AC上做平行四边形AKLC，使它与△ABC位于AC的同侧，再以AB和BC为底作平行四边形AEFB和BMNC，使它们与△ABC分别位于AB和BC的两侧，并使EF经过K，MN经过L，猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系，并说明理由．

    查看答案和解析>>

    同步练习册答案