
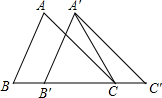
 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
分析 根据平移的性质可得A′B′=AB,∠A′B′C′=∠B,再求出B′C,过点A′作A′D⊥B′C于D,再求出A′D,然后根据三角形的面积公式列式计算即可得解.
解答  解:∵△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,
解:∵△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,
∴A′B′=AB=4,∠A′B′C′=∠B=60°,
B′C=6-2=4,
过点A′作A′D⊥B′C于D,
则A′D=$\frac{\sqrt{3}}{2}$A′B′=$\frac{\sqrt{3}}{2}$×4=2$\sqrt{3}$,
∴△A′B′C的面积=$\frac{1}{2}$B′C•A′D=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$.
故选C.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{32}$ | C. | $\sqrt{18}$ | D. | $\sqrt{75}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
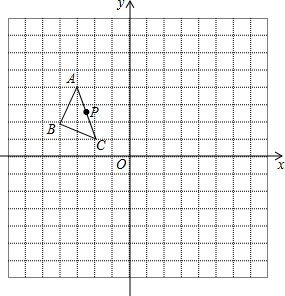 如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
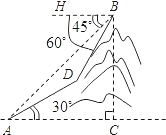 如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).
如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com