
【题目】如图,在 ![]() ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
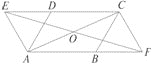
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
【答案】(1)证明见解析(2)成立
【解析】(1)由已知条件可得△AED,△CFB是正三角形,可得∠AEC=∠BFC=60°,∠EAF=∠FCE=120°,所以四边形AFCE是平行四边形.
(2)上述结论还成立,可以证明△ADE≌△CBF,可得∠AEC=∠BFC,∠EAF=∠FCE,所以四边形AFCE是平行四边形.
解:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°.
∴∠ADE=∠CBF=60°.
∵AE=AD,CF=CB,
∴△AED,△CFB是正三角形.
∴∠AEC=∠BFC=60°,∠EAF=∠FCE=120°.
∴四边形AFCE是平行四边形.
(2)解:上述结论还成立.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠CDA=∠CBA,∠DCB=∠DAB,AD=BC,DC=AB.
∴∠ADE=∠CBF.
∵AE=AD,CF=CB,
∴∠AED=∠ADE,∠CFB=∠CBF.
∴∠AED=∠CFB.
又∵AD=BC,
在△ADE和△CBF中.
∠ADE=∠CBF,∠AED=∠CFB,AD=BC,
∴△ADE≌△CBF(AAS).
∴∠AED=∠BFC,∠EAD=∠FCB.
又∵∠DAB=∠BCD,
∴∠EAF=∠FCE.
∴四边形EAFC是平行四边形.


科目:初中数学 来源: 题型:
【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
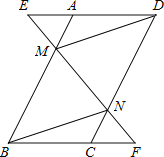
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB上的点,且A1C1∥AC,A1B1∥AB,B1C1∥BC,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1上的点,且A2C2∥A1C1,A2B2∥A1B1,B2C2∥B1C1,…,按此规律,则第n个图形中平行四边形的个数共有__个.
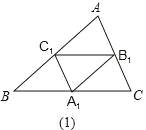
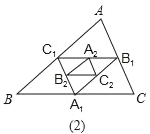

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( ) 
A.πcm2
B.![]() πcm2
πcm2
C.![]() cm2
cm2
D.![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D. 
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( )
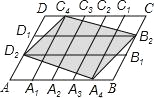
A. 2 B. ![]() C.
C. ![]() D. 15
D. 15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com