练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”

    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等，

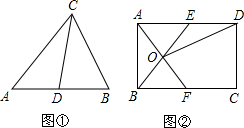
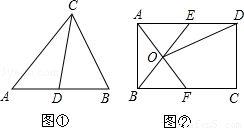
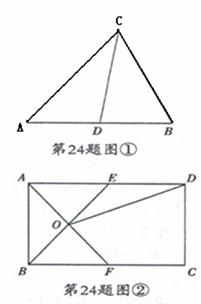
    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD＝S△BCD．

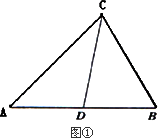
    应用：如图②，在矩形ABCD中，AB＝4，BC＝6，点E在AD上，点F在BC上，AE＝BF，AF与BE交于点O，

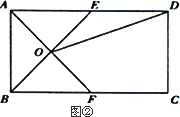
    (1)求证：△AOB和△AOE是“友好三角形”；

    (2)连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积，

    探究：在△ABC中，∠A＝30°，AB＝4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•沈阳）定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．
    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．
    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．
    应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
    （1）求证：△AOB和△AOE是“友好三角形”；
    （2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．
    探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得
    到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的
    14
    ，请直接写出△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（辽宁沈阳卷）数学（解析版） 题型：解答题

    定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．

    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．

    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．

    应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．

    （1）求证：△AOB和△AOE是“友好三角形”；

    （2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．

    探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2013年辽宁省沈阳市中考数学试卷（解析版） 题型：解答题

    定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．
    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．
    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．
    应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
    （1）求证：△AOB和△AOE是“友好三角形”；
    （2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．
    探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得
    到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．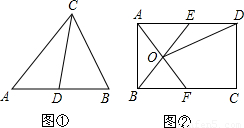

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”

      性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等，

      理解：如图①，在中，CD是AB边上的中线，那么和是“友好三角形”，并且。

      应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O，

    （1）       求证: 和是“友好三角形”；

    （2）       连接OD，若和是“友好三角形”，求四边形CDOF的面积，

      探究：在中，，AB=4，点D在线段AB上，连接CD，和是“友好三角形”，将沿CD所在直线翻折，得到与重合部分的面积等于面积的，请直接写出的面积。

    查看答案和解析>>

    同步练习册答案