
分析 (1)根据材料1,用换元法进行分解因式;
(2)根据材料1,用换元法进行分解因式;
(1)根据材料2,用换元法进行分解因式.
解答 解:(1)设t=a2,则原式=t2-18t+81=(t-9)2=(t-3)2(t+3)2;
(2)∵(x-3)(x+6)=x2+3x-18,(x-2)(x+9)=x2+7x-18,
设A=x2+3x-18,
∴原式=A(A+4x)+4x2=A2+4Ax+4x2=(A+2x)2=(x2+5x-18)2;
(3)原式=x2(x2-4x+2+$\frac{4}{x}$+$\frac{1}{{x}^{2}}$)=x2[(x2+$\frac{1}{{x}^{2}}$)-4(x-$\frac{1}{x}$)+2],
设t=x-$\frac{1}{x}$,
则原式=x2(t2-4t+4)=x2(t-2)2=x2(x-$\frac{1}{x}$-2)2.
点评 本题考查了因式分解-十字相乘法,公式法,熟练掌握因式分解的方法是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角45°,他在二楼窗台B处测得M的仰角31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度(结果保留两位小数)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角45°,他在二楼窗台B处测得M的仰角31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度(结果保留两位小数)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
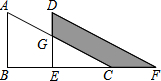 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com