
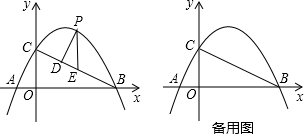
���� ��1����y=a��x+1����x-4������C��0��2���������a��ֵ���ɣ�
��2���ӳ�PE��x�����F�����ݹ��ɶ��������BC�ij���Ȼ����֤����PDE�ס�BOC���������������ε����ʿ����PE=2�����BC�Ľ���ʽΪy=-$\frac{1}{2}$x+2�����P������Ϊ��x��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2������E��x��-$\frac{1}{2}$x+2��������PE=2�ɵõ�����x�ķ��̣��Ӷ�����õ�P�����ꣻ
��3���ȸ������⻭��ͼ�Σ�Ȼ������ֱ��������б�������ߵ����ʿ����P��N=1������D����D��H��P��E�䣬�����D��H�ij����Ӷ��õ�P��H�ij���Ȼ������NH�ij�����D�䣨x��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2������N��x-$\frac{3}{5}$��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2+$\frac{4}{5}$������N���������ߵĽ���ʽ�����x��ֵ���Ӷ��õ���D�ĺ����꣮
��� �⣺��1����y=a��x+1����x-4������C��0��2��������a=$-\frac{1}{2}$
��y=-$\frac{1}{2}$��x+1����x-4��=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����ͼ1��ʾ���ӳ�PE��x�����F��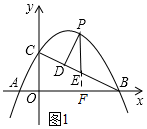
��OC=2��OB=4��
��BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=2$\sqrt{5}$��
��PD��BC��CO��OB��
���COB=��PDE=90�㣮
�ߡ�PDE=��EFB����PED=��FEB��
���DPE=��CBO��
���PDE�ס�BOC��
��$\frac{DE}{PE}$=$\frac{OC}{BC}$����$\frac{\frac{2\sqrt{5}}{5}}{PE}$=$\frac{2}{2\sqrt{5}}$�����PE=2��
��BC�Ľ���ʽΪy=kx+2������B���������ã�4k+2=0����ã�k=-$\frac{1}{2}$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
���P��������x��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2������E��x��-$\frac{1}{2}$x+2����
��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2-��-$\frac{1}{2}$x+2��=2�����x1=x2=2��
���P��������2��3����
��3����ת���ͼ����ͼ2��ʾ������D����D��H��P��E�䣬����ΪH��
�ߡ�P'D'E'=90�㣬N��б��P'E'���е㣬
��D��B=$\frac{1}{2}$P��E��=1��
��$\frac{1}{2}$P��D��•E��D��=$\frac{1}{2}$P��E��•HD�䣬
��D��H=$\frac{P��D���D��E��}{P��E��}$=$\frac{\frac{4\sqrt{5}}{5}��\frac{2\sqrt{5}}{5}}{2}$=$\frac{4}{5}$��
��HP��=$\frac{8}{5}$��
��HN=P��H-P��N=$\frac{3}{5}$��
��D�䣨x��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2������N��x-$\frac{3}{5}$��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2+$\frac{4}{5}$����
��N��������������ߵ�-$\frac{1}{2}$x2+$\frac{3}{2}$x+2+$\frac{4}{5}$=-$\frac{1}{2}$��x-$\frac{3}{5}$��2+$\frac{3}{2}$��x-$\frac{3}{5}$��+2����ã����x=$\frac{47}{15}$��
���D��ĺ�����Ϊ$\frac{47}{15}$��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ�����������ε����ʺ��ж����г�PE�ij����P������֮��ĺ�����ϵʽ������⣨2���Ĺؼ����ú�x��ʽ�ӱ�ʾ����N�������ǽ�����⣨3���Ĺؼ���


 Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
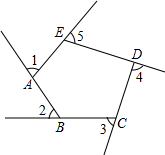 ��ͼ��1����2����3����4����5�������ABCDE����ǣ���1=��2=��3=��4=70�㣬���AED=100�㣮
��ͼ��1����2����3����4����5�������ABCDE����ǣ���1=��2=��3=��4=70�㣬���AED=100�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
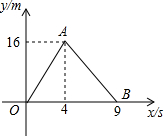 �����ܵ��������ܲ�������õܵ����ܣ���ͼ��ʾ����������֮��ľ���y��ʱ��x֮��ĺ���ͼ����ͼ����Ϣ�ش��������⣮
�����ܵ��������ܲ�������õܵ����ܣ���ͼ��ʾ����������֮��ľ���y��ʱ��x֮��ĺ���ͼ����ͼ����Ϣ�ش��������⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��2 | B�� | ��-3��-��-3�� | C�� | 2��3 | D�� | 2����-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12-4k | B�� | 6 | C�� | -6 | D�� | 4k-12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ס���������Լ��ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ������˵����ȷ�ĸ���Ϊ��������
�ס���������Լ��ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ������˵����ȷ�ĸ���Ϊ��������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com