练习册

  • 练习册
  • 试题
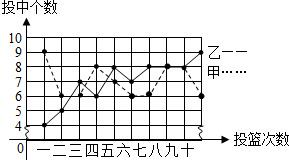
    精英家教网 > 初中数学 > 题目详情
    甲、乙两个同学根据下列条件画三角形，他们画出的三角形一定全等的条件是（　　）
    分析：如果画法符合全等三角形的判定方法：SSS，SAS，AAS，则画出的三角形一定全等，据此作答．
    解答：解：A、B、只有两个条件，不符合全等三角形的判定方法，故本选项错误；
    C、SSA在直角和钝角的情况下成立，故本选项正确；
    D、由C可得，本选项错误．
    故选C．
    点评：此题主要考查全等三角形的判定方法，容易出错的是SSA的形式，注意：只有在直角和钝角的情况下成立．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某校高中一年级组建篮球队，对甲、乙两名备选同学进行定位投篮测试，每次投10个球共投10次，甲、乙两名同学测试情况如图所示．
    精英家教网
    （1）根据如图所提供的信息填写下表：
    平均数 众数 方差
    甲 1.2
    乙 2.2
    （2）如果你是高一学生会文体委员，会选择哪名同学进入篮球队？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、某班实行小组量化考核制．为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：
    综合评价得分统计表（单位：分）
    周次
    组别    		 一 二 三 四 五 六
    甲组 12 15 16 14 14 13
    乙组 9 14 10 17 16 18
    （1）请根据表中的数据完成下表（注：方差的计算结果精确到0.1）
    平均数 中位数 方差
    甲组 14
    乙组 14 11.7
    （2）根据综合评价得分统计表中的数据，请在下图中画出乙组综合评价得分的折线统计图．
    （3）根据折线统计图中的信息，请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•广阳区一模）甲、乙两组同学进行一分钟引体向上测试，评分标准规定，做6个以上（含6个）为合格，做9个以上（含9个）为优秀，两组同学的测试成绩如下表：
    成绩（个） 4 5 6 7 8 9
    甲组（人） 1 2 5 2 1 4
    乙组（人） 1 1 4 5 2 2
    （1）小明根据两组同学的测试成绩绘制了条形统计图，请你将缺少的部分补充完成；
    （2）小斌对两组同学的测试成绩进行了如下的统计分析，请将下表补充完整：
    统计量 平均数（个） 中位数 众数 方差 合格率 优秀率
    甲组 6.8 6 2.56 26.7%
    乙组 6.8 7 1.76 86.7% 13.3%
    （3）甲组学生说两组同学引体向上的平均个数相同、优秀率高于乙组，所以他们的成绩好于乙组，但乙组学生不同意这种说法，请你给出三条支持乙组学生观点的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    数学活动课上，甲、乙两位同学在研究一道数学题：“已知：如图1，在△ABC和△DEF中，∠A=∠D=90°，∠B=50°，∠E=32°，且BC=EF．试画直线m，l，使直线m将△ABC分成的两个小三角形与直线l将△DEF分成的两个小三角形分别相似，并标出每个小三角形各内角的度数．”
    甲同学是这样做的：如图2，使得两个直角三角形的斜边重合，以斜边中点0为圆心，OB长为半径作出辅助圆，根据到定点的距离等于定长的点在圆上，可知A、B（E）、C（F）、D在⊙0上．设BD所在的直线m与AC所在的直线l交于点G，根据同弧所对的圆周角相等，由∠ABC=50°，∠DEF=32°，易求得∠ABG=DFG=18°，再由∠A=∠D=90°，可求得∠AGB=∠DGF=72°，∠GCB=40°，∠BGC=108°，从而△AGB∽△DGF．△GBC∽△GEF．
    乙同学在甲同学的启发下，利用辅助圆又补充了其它分割方法．
    你看明白甲同学的分割方法了吗？请你仿照甲同学的方法，把这道题其它的所有分割方法补充完整．
    要求：不需写解答过程．如图2所示．利用辅助圆画出示意图，标明直线及每个小三角形各内角的度数即可．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答．
    方案一：甲队单独完成这项工程刚好能够如期完成；
    方案二：乙队单独完成这项工程要比规定的时间多用10天；
    方案三：若甲、乙两队合作8天，余下的由乙队单独做也正好如期完成．
    又从甲、乙两个工程队的投标书中得知：每天需支付甲队的工程款1.5万元，乙队的工程款1.1万元．
    试问，在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？请说明理由．
    解题方案：
    设甲队单独完成需x天，则乙队单独完成需（x+10）天．
    （1）用含x的代数式表示：
    甲队每天可以完成这项工程的工作量是工程总量的
    1
    x
    1
    x

    乙队每天可以完成这项工程的工作量是工程总量的
    1
    x+10
    1
    x+10

    根据题意，列出相应方程
    8
    x
    +
    x
    x+10
    =1
    8
    x
    +
    x
    x+10
    =1

    解这个方程，得
    x=40
    x=40

    检验：
    x=40是原方程的根
    x=40是原方程的根

    （2）方案一得工程款为
    40×1.5=60（万元）
    40×1.5=60（万元）
    ；
    方案二不合题意，舍去
    方案三的工程款为
    8×1.5+40×1.1=56（万元）
    8×1.5+40×1.1=56（万元）

    所以在不耽误工期的前提下，应选择方
    （3）
    （3）
    能节省工程款．

    查看答案和解析>>

    同步练习册答案