
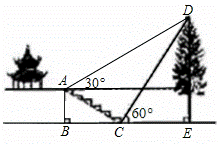
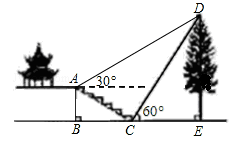
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
考点:
解直角三角形的应用-仰角俯角问题.
分析:
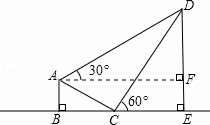
过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
解答:
解:如图,过点A作AF⊥DE于F,
则四边形ABEF为矩形,
∴AF=BE,EF=AB=3,
设DE=x,
在Rt△CDE中,CE=![]() =
=![]() x,
x,
在Rt△ABC中,
∵![]() =
=![]() ,AB=3,
,AB=3,
∴BC=3![]() ,
,
在Rt△AFD中,DF=DE﹣EF=x﹣3,
∴AF=![]() =
=![]() (x﹣3),
(x﹣3),
∵AF=BE=BC+CE,
∴![]() (x﹣3)=3
(x﹣3)=3![]() +
+![]() x,
x,
解得x=9.
答:树高为9米.
点评:
本题考查了解直角三角形的应用,解题的关键是正确的构造直角三角形并选择正确的边角关系解直角三角形,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
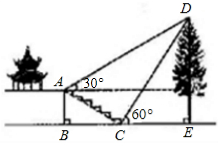 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1:
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1:| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
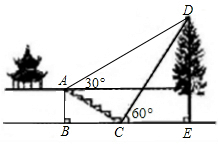 (2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:
(2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为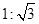 (即AB:BC=
(即AB:BC=![]() ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
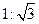 (即AB:BC=
(即AB:BC=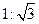 ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).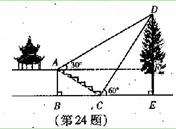
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川内江卷)数学(解析版) 题型:解答题
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为 (即AB:BC=
(即AB:BC= ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com