
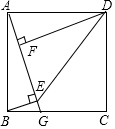
 如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.分析 (1)由∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,推出∠BAE=∠ADF,即可根据AAS证明△ABE≌△DAF;
(2)设EF=x,则AE=DF=x+1,根据四边形ABED的面积为6,列出方程即可解决问题;
解答 证明:(1)∵ 四边形ABCD是正方形,
四边形ABCD是正方形,
∴AB=AD,
∵DF⊥AG,BE⊥AG,
∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中,
$\left\{\begin{array}{l}{∠BAE=∠ADF}\\{∠AEB=∠DFA}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△DAF(AAS).
(2)设EF=x,则AE=DF=x+1,
由题意2×$\frac{1}{2}$×(x+1)×1+$\frac{1}{2}$×x×(x+1)=6,
解得x=2或-5(舍弃),
∴EF=2.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程,属于中考常考题型.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:填空题
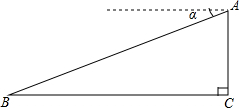 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
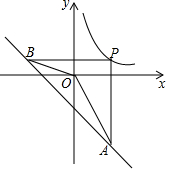 如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )
如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5×108 | B. | 1.5×109 | C. | 0.15×109 | D. | 15×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com