
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
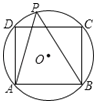
A.45° B.60° C.45° 或135° D.60° 或120°
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)下列事件是不可能事件的是
A.选购甲品牌的B型号;
B.选购甲品牌的C型号和乙品牌的D型号;
C.既选购甲品牌也选购乙品牌;
D.只选购乙品牌的E型号.
(2)用列表法或树状图法,写出所有的选购方案,若每种方案被选中的可能性相同,求A型号的器材被选中的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD中,AB=5,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F.
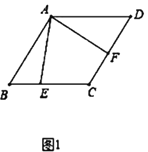
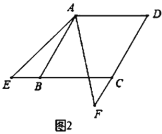
(1)如图1所示,当点E、F分别在边BC、CD上时,求CE+CF的值;
(2)如图2所示,当点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 的延长线时,请从
的延长线时,请从![]() ,
,![]() 两题中任选一题作答,我选______题.
两题中任选一题作答,我选______题.
![]() 题:则
题:则![]() 的值是________.
的值是________.
![]() 题:则
题:则![]() 与
与![]() 的关系是________.
的关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=135°;④BC+FG=
;③∠AFG=135°;④BC+FG=![]() .其中正确的结论是_____.(填入正确的序号)
.其中正确的结论是_____.(填入正确的序号)
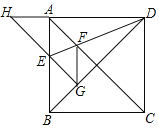
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选择家用净水器,光明商场计划从生产厂家购进甲、乙两种型号的家用净水器,甲型号净水器进价为160元/台,乙型号净水器进价为280元/台,经过协商沟通,生产厂家拿出了两种优惠方案:第一种优惠方案:甲、乙两种型号净水器均按进价的8折收费;第二种优惠方案:甲型号净水器按原价收费,乙型号净水器的进货量超过10台后超过的部分按进价的6折收费.
光明商场只能选择一种优惠方案,已知光明商场计划购进甲型号净水器数量是乙型号净水器数量的1.5倍,设光明商场购进乙型号净水器![]() 台,选择第一种优惠方案所需费用为片
台,选择第一种优惠方案所需费用为片![]() 元,选择第二种优惠方案所需费用为
元,选择第二种优惠方案所需费用为![]() 元.
元.
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式:
的关系式:
(2)光明商场计划购进乙型号净水器40台,请你为光明商场选择合适的优惠方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
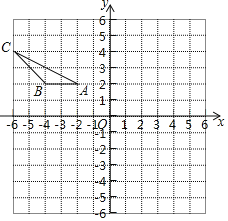
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣4,2),C(﹣6,4),先将△ABC沿一确定方向平移得到△A1B1C1,点C的对应点为点C1的坐标是(﹣4,﹣2),再将△A1B1C1将绕点O逆时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求在这两次变过程中,点B经过点B1到达点B2的路径总长(结果保留π);
(4)△A2B2C2可看成将△ABC以某点为旋转中心,逆时针旋转90°而得,则旋转中心的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
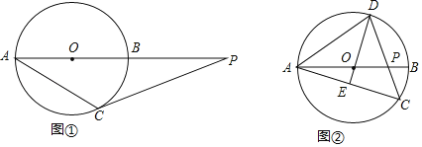
【题目】在⊙O中,AB为直径,C为⊙O上一点.
(Ⅰ)如图①,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=32°,求∠P的大小;
(Ⅱ)如图②,D为优弧ADC上一点,且DO的延长线经过AC的中点E,连接DC与AB相交于点P,若∠CAB=16°,求∠DPA的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
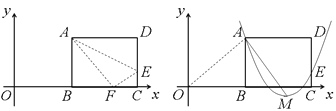
【题目】如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
(1)求点E、F的坐标(用含m的式子表示);(5分)
(2)连接OA,若△OAF是等腰三角形,求m的值;(4分)
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值. (5分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com