
【题目】如图1,Rt△ACB 中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)利用直尺和圆规在图1中画出⊙O(不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断BD所在直线与(1)中所作的⊙O的位置关系,并证明你的结论;
(3)设⊙O交AB于点E,连接DE,过点E作EF⊥BC,F为垂足,若点D是线段AC的黄金分割点(即 ![]() =
= ![]() ),如图2,试说明四边形DEFC是正方形).
),如图2,试说明四边形DEFC是正方形).
【答案】
(1)解:如图1,⊙O为所作;
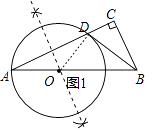
(2)解:BD与⊙O相切.理由如下:
连接OD,如图1,
∵OA=OD,
∴∠A=∠ODA,
∵∠CBD=∠A,
∴∠CBD=∠ODA,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∴∠ODA+∠CDB=90°,
∴∠ODB=90°,
∴OD⊥BD,
∴BD为⊙O的切线;
(3)解:∵∠CBD=∠A,∠DCB=∠BCA,
∴△CDB∽△CBA,
∴CD:CB=CB:CA,
∴CB2=CDCA,
∵点D是线段AC的黄金分割点, 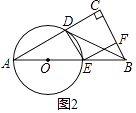
∴AD2=CDAC,
∵AD=CB,
∵AE为直径,
∴∠ADE=90°,
在△ADE和△BCD中
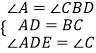 ,
,
∴△ADE≌△BCD,
∴DE=DC,
∵EF⊥BC,
∴∠EFC=90°,
∴四边形CDEF为矩形,
∴四边形DEFC是正方形.
【解析】(1)过A、D的圆圆心在AD的垂直平分线上,由交轨法,必在此线与AB的交点处;(2)要证相切,须连结半径,再证∠ODB=90°,可利用已知的∠C=90°,∠CBD=∠A即可证出;(3)由(2)中的△CDB∽△CBA可得CB2=CDCA,由已知“点D是线段AC的黄金分割点”可得AD2=CDAC,两式比较可得AD=CB,进而证得全等,所以DE=DC,易证四边形CDEF为矩形,即可证得四边形DEFC是正方形.


科目:初中数学 来源: 题型:
【题目】某校举行学生“爱校·爱家·爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:

①共有10人得6分;
②得5分和7分的人数一样多;
③8名选手的成绩高于8分;
④共有25名选手参赛.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的身体素质情况,随机对九年级的50名学生进行一分钟跳绳次数测验,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | a |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a+10 |
第5组 | 160≤x<180 |
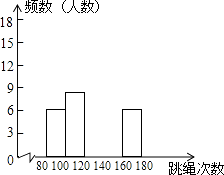
请结合图表完成以下问题.
(1)求出表中的a;
(2)补全频数分布直方图;
(3)若x≥140为优良,该校九年级有450名学生,请估计跳绳成绩达到优良的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足|a-![]() |+
|+![]() +(c-
+(c-![]() )2=0.
)2=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能,求出其周长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=![]() BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
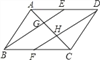
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD= ![]() ,请求出AC的长.
,请求出AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com