
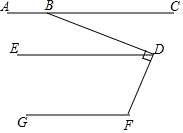
 如图,已知AC∥ED,ED∥GF,∠BDF=90°.
如图,已知AC∥ED,ED∥GF,∠BDF=90°.分析 (1)根据平行线的性质可得∠ABD+∠BDE=180°,进而可得∠BDE=30°,然后再计算出∠EDF的度数,再根据平行线的性质可得∠EDF+∠F=180°,进而可得∠GFD的度数;
(2)与(1)类似,表示出∠F的度数,再表示出∠CBD的度数,再求差即可.
解答 解:(1)∵AC∥ED,
∴∠ABD+∠BDE=180°,
∵∠ABD=150°,
∴∠BDE=30°,
∵∠BDF=90°,
∴∠EDF=60°,
∵ED∥GF,
∴∠EDF+∠F=180°,
∴∠F=120°;
(2)∵AC∥ED,
∴∠ABD+∠BDE=180°,
∵∠ABD=θ,
∴∠BDE=θ,
∵∠BDF=90°,
∴∠EDF=(90-θ)°,
∵ED∥GF,
∴∠EDF+∠F=180°,
∴∠F=(90+θ)°,
∵∠ABD=θ,
∴∠CBD=(180-θ)°,
∴∠GFD-∠CBD=(90+θ)°-(180-θ)°=(2θ-90)°.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,同旁内角互补.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
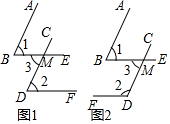 在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结论图形完成以下探究过程:
在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结论图形完成以下探究过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
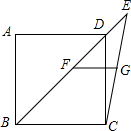 如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG.若AB=6,则FG的长度为( )
如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG.若AB=6,则FG的长度为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com