
【题目】已知A和B两点在线段EF的中垂线上,且∠EBF=100°,∠EAF=70°,则∠AEB等于( )
A.95°
B.15°
C.95°或15°
D.170°或30°
【答案】C
【解析】解答:如图(1),当点A、B在线段EF的同侧时,∵A和B两点在线段EF的中垂线上,∴AE=AF,BE=BF,又∵∠EBF=100°,∠EAF=70°,∴∠AEF=∠AFE=55°,∠BEF=∠BFE=40°,∴∠AEB=∠AEF-∠BEF=15°;如图(2),当点A、B在线段EF的两侧时,∵A和B两点在线段EF的中垂线上,∴AE=AF,BE=BF,又∵∠EBF=100°,∠EAF=70°,∴∠AEF=∠AFE=55°,∠BEF=∠BFE=40°,∴∠AEB=∠AEF+∠BEF=95°.故选C.

分析:本题没有给出图形,所以需要考虑点A、B在线段EF的同侧与两侧来解题.
【考点精析】通过灵活运用线段垂直平分线的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
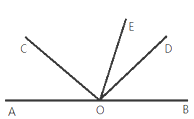
【题目】如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
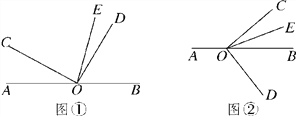
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
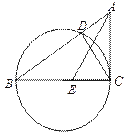
【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=![]() ,tan∠AEC=
,tan∠AEC=![]() ,求圆的直径.
,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3
B.∠1=∠2
C.∠2=∠3
D.∠1=∠2=∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三连个月投放单车数量的月平均增长率为x,则所列方程正确的是( )
A.1000(1+x)2=440B.1000(1+x)2=1000
C.1000(1+2x)=1000+440D.1000(1+x)2=1000+440
查看答案和解析>>
科目:初中数学 来源: 题型:
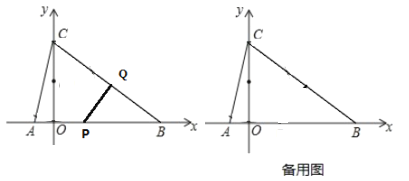
【题目】如图,在平面直角坐标系中,O是坐标原点,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
(1)求抛物线的解析式及点A的坐标;
(2)在点P从点A出发的同时,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒![]() 个单位长度的速度向点A运动,运动时间和点P相同.
个单位长度的速度向点A运动,运动时间和点P相同.
①记△BPQ的面积为S,当t为何值时,S最大,最大值是多少?
②是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在同一直线上,且AB:BC:CD=2:3:5
(1)若AD=24cm,求AB、BC、CD的长;
(2)若点M、N是AC、CD中点,且AD=a,求MN的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com