
分析 (1)根据负整数指数幂、零指数幂即可解答本题;
(2)根据同底数幂的乘法和除法即可解答本题;
(3)根据多项式乘多项式、完全平方公式即可解答本题;
(4)根据完全平方公式即可解答本题.
解答 解:(1)(-$\frac{1}{2}$)-1-2+(π-3.14)0-(-2)-3
=(-2)-2+1+$\frac{1}{8}$
=$-2\frac{7}{8}$;
(2)(x2-2xy)•9x2-(9xy3-12x4y2)÷3xy
=9x4-18x3y-3y2+4x3y
=9x4-14x3y-3y2;
(3)(x+5)(x-1)+(x-2)2
=x2+4x-5+x2-4x+4
=2x2-1;
(4)1022
=(100+2)2
=1002+400+4
=10000+400+4
=10404.
点评 本题考查整式的混合运算、负整数指数幂、零指数幂,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
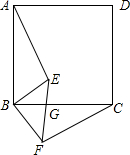 如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 连接两点的线段的长度叫做这两点间的距离 | |
| B. | 两直线平行,同旁内角互补 | |
| C. | 若两个角有公共顶点且有一条公共边,和等于平角,则这两个角互为邻补角 | |
| D. | 平移变换中,连接各组对应点所得线段平行且相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{{v_1}+{v_2}}}{2}$ | B. | $\frac{{2\;{v_1}{v_2}}}{{{v_1}+{v_2}}}$ | C. | $\frac{2}{{{v_1}+{v_2}}}$ | D. | $\frac{{{v_1}+{v_2}}}{{2\;{v_1}{v_2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com