练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图的平面直角坐标系中有一个正六边形ABCDEF，其中C、D的坐标分别为(1，0)和(2，0)．若在无滑动的情况下，将这个六边形沿着x轴向右滚动，则在滚动过程中，这个六边形的顶点A、B、C、D、E、F中，会过点(45，2)的是点________．

    答案：B
    解析：

    因为C、D两点坐标分别为(1，0)、(2，0)，所以按题中滚动方法点E经过点(3，0)，点F经过点(4，0)，点A经过点(5，0)，点B经过(6，0)．因为六边形的边长为1，所以而该六边形中AD＝BE＝CF＝2，而点(45，0)的横坐标是6的倍数多3，，该六边形滚动6次正好一周，故可知经过(45，0)的点经过(3，0)，所以点E经过点(45，0)，因为BE＝2，所以点B经过点(45，2)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某校九年级的一场篮球比赛中，如图队员甲正在投篮，已知球出手时离地面高
    209
    m，与篮圈中心的水平距离7m．当球出手后水平距离为4m时到达最大高度4m，设篮球运行的轨迹为抛物线，篮圈距地面3m．
    （l）建立如图的平面直角坐标系，求出此轨迹所在抛物线的解析式．
    （2）问此球能否准确投中？
    （3）此时，若对方队员乙在甲前面2m 处跳起盖帽拦截，已知乙的最大摸高为3．lm，那么他能否拦截成功？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图①，矩形ABCD被对角线AC分为两个直角三角形，AB=3，BC=6．现将Rt△ADC绕点C顺时针旋转90°，点A旋转后的位置为点E，点D旋转后的位置为点F．以C为原点，以BC所在直线为x轴，以过点C垂直于BC的直线为y轴，建立如图②的平面直角坐标系．

    （1）求直线AE的解析式；
    （2）将Rt△EFC沿x轴的负半轴平行移动，如图③．设OC=x（0＜x≤9），Rt△EFC与Rt△ABO的重叠部分面积为s；求当x=1与x=8时，s的值；
    （3）在（2）的条件下s是否存在最大值？若存在，求出这个最大值及此时x的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将边长为4的正方形在如图的平面直角坐标系中．点P是OA上的一个动点，且从点O向点A运动．连接CP交对角线OB于点D，连接AD．
    （1）求证：△OCD≌△OAD；
    （2）若△OCD的面积是四边形OABC面积的
    16
    ，求P点的坐标；
    （3）若点P从点O运动到点A后，再继续从点A运动到点B，在整个运动过程中，当△OCD恰为等腰三角形时，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在如图的平面直角坐标系中，依次描出下列各点：
    （0，2），（5，6），（3，2），（5，3），（5，1），（3，2），（4，0），（0，2）．
    再用线段顺次连接各点，得到一个图形象
    一条鱼
    一条鱼
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

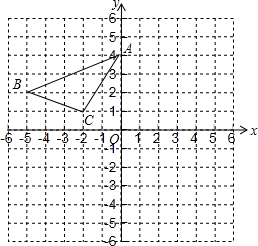    精英家教网△ABC在如图的平面直角坐标系中，将其平移得到△A'B'C'，若B的对应点B′的坐标为（1，1）；
    （1）在图中画出△A′B′C′；
    （2）此次平移可以看作将△ABC向
     
    平移
     
    个单位长度，再向
     
    平移
     
    个单位长度，得△A′B′C′；
    （3）直接写出△A′B′C′的面积为
     
    ．

    查看答案和解析>>

    同步练习册答案