
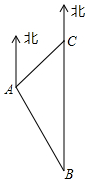
 如图,某渔船航行至B处时,侧得一海岛位于B处的正北方向20(1+$\sqrt{3}$)海里的C处,为了防止意外,渔船请求A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位子B的北偏西300的方向上,求A,C之间的距离.
如图,某渔船航行至B处时,侧得一海岛位于B处的正北方向20(1+$\sqrt{3}$)海里的C处,为了防止意外,渔船请求A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位子B的北偏西300的方向上,求A,C之间的距离. 分析 作AD⊥BC,设CD=x,根据正切的概念用x表示出AD、BD,根据题意列出方程,解方程即可.
解答 解:作AD⊥BC,垂足为D,
由题意得,∠ACD=45°,∠ABD=30°,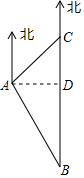
设CD=x,
在Rt△ACD中,AD=CD=x,
在Rt△ABD中,可得BD=$\frac{AD}{tan∠B}$=$\sqrt{3}$x,
∵BC=20,
∴x+$\sqrt{3}$x=20(1+$\sqrt{3}$),
解得:x=20,
∴AC=20$\sqrt{2}$,
答:A、C之间的距离为20$\sqrt{2}$海里.
点评 本题考查的是解直角三角形的应用-方向角问题,方向角的概念、熟记锐角三角函数的定义是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
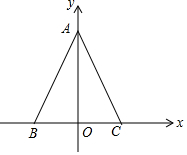 如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).
如图,在直角坐标系中,A(0,4),B(-2,0),C(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )| A. | $\sqrt{74}$ | B. | $\sqrt{74}$+3 | C. | $\sqrt{74}$-3 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
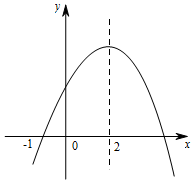 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)2a+b=0;(2)9a+c>3b;(3)5a+7b+2c>0;(4)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y2<y3;(5)若方程a(x+1)(x-5)=c的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)2a+b=0;(2)9a+c>3b;(3)5a+7b+2c>0;(4)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y2<y3;(5)若方程a(x+1)(x-5)=c的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 110° | B. | 30° | C. | 110°或150° | D. | 30°或110° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com