

 œâŁșŁš1Ł©ĄßĄÏOAB=45ĄăŁŹĄÏAOB=90ĄăŁŹOB=6ŁŹ
œâŁșŁš1Ł©ĄßĄÏOAB=45ĄăŁŹĄÏAOB=90ĄăŁŹOB=6ŁŹ ŁŹ
ŁŹ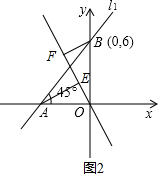 ĄàĄÏAOE=ĄÏFBOŁŹ
ĄàĄÏAOE=ĄÏFBOŁŹ ŁŹ
ŁŹ ŁŹ
ŁŹ 5Ł©ÁȘÁąșŻÊęl1ÓëșŻÊęl2żÉ”ĂŁș
5Ł©ÁȘÁąșŻÊęl1ÓëșŻÊęl2żÉ”ĂŁș ŁŹ
ŁŹ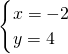 ŁŹ
ŁŹ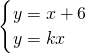 ŁŹ
ŁŹ ŁŹ
ŁŹ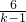 ŁŹ
ŁŹ Ł©ŁŹ
Ł©ŁŹ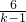 ʱŁŹy=x+6ŁŸ4ŁŹ
ʱŁŹy=x+6ŁŸ4ŁŹ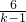 ʱŁŹy=
ʱŁŹy= =6+
=6+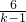 ŁŸ6Ł»
ŁŸ6Ł»


| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 ÈçÍŒŁŹÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹOÎȘÖ±œÇÈęœÇĐÎABC”ÄÖ±œÇ¶„”㣏ĄÏB=30ĄăŁŹÈńœÇ¶„”ăAÔÚË«ÇúÏßy=
ÈçÍŒŁŹÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹOÎȘÖ±œÇÈęœÇĐÎABC”ÄÖ±œÇ¶„”㣏ĄÏB=30ĄăŁŹÈńœÇ¶„”ăAÔÚË«ÇúÏßy=| 1 | x |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 =2
=2| 3 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
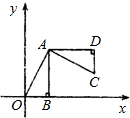 ÈçÍŒŁŹÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹOBÔÚxÖáÉÏŁŹĄÏABO=90ĄăŁŹ”ăA”ÄŚű±êÎȘŁš1ŁŹ2Ł©Łźœ«ĄśAOBÈÆ”ăAÄæʱŐëĐęŚȘ90ĄăŁŹÔò”ăO”ĶÔÓŠ”ăC”ÄŚű±êÎȘŁšĄĄĄĄŁ©
ÈçÍŒŁŹÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹOBÔÚxÖáÉÏŁŹĄÏABO=90ĄăŁŹ”ăA”ÄŚű±êÎȘŁš1ŁŹ2Ł©Łźœ«ĄśAOBÈÆ”ăAÄæʱŐëĐęŚȘ90ĄăŁŹÔò”ăO”ĶÔÓŠ”ăC”ÄŚű±êÎȘŁšĄĄĄĄŁ©Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
| a+2 |
| SĄśCAD |
| SĄśDGH |
| AD |
| GH |
| FC+2AE |
| 3AM |

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
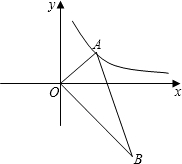
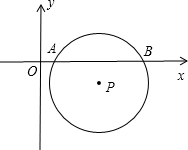
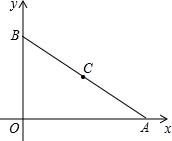 ÈçÍŒÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹA”ăŚű±êÎȘŁš8ŁŹ0Ł©ŁŹB”ăŚű±êÎȘŁš0ŁŹ6Ł©CÊÇÏ߶ÎAB”ÄÖД㣟ÇëÎÊÔÚyÖáÉÏÊÇ·ńŽæÔÚÒ»”ăPŁŹÊč”ĂÒÔPĄąBĄąCÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜AOBÏàËÆŁżÈôŽæÔÚŁŹÇółöP”ăŚű±êŁ»ÈôČ»ŽæÔÚŁŹË”ĂśÀíÓÉŁź
ÈçÍŒÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹA”ăŚű±êÎȘŁš8ŁŹ0Ł©ŁŹB”ăŚű±êÎȘŁš0ŁŹ6Ł©CÊÇÏ߶ÎAB”ÄÖД㣟ÇëÎÊÔÚyÖáÉÏÊÇ·ńŽæÔÚÒ»”ăPŁŹÊč”ĂÒÔPĄąBĄąCÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜AOBÏàËÆŁżÈôŽæÔÚŁŹÇółöP”ăŚű±êŁ»ÈôČ»ŽæÔÚŁŹË”ĂśÀíÓÉŁźČ鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com