
【题目】如图,直线l![]() 在平面直角坐标系中,直线l
在平面直角坐标系中,直线l![]() 与y轴交于点A,点B(-3,3)也在直线1上,将点B先向右平移1个单位长度、再向下平移2个单位长度得到点C,点C恰好也在直线l
与y轴交于点A,点B(-3,3)也在直线1上,将点B先向右平移1个单位长度、再向下平移2个单位长度得到点C,点C恰好也在直线l![]() 上。
上。
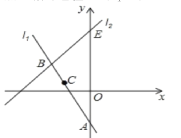
(1)求点C的坐标和直线l![]() 的解析式
的解析式
(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l![]() 上;
上;
(3)已知直线l![]() :y=x+b经过点B,与y轴交于点E,求△ABE的面积。
:y=x+b经过点B,与y轴交于点E,求△ABE的面积。
【答案】(1)(-2,1),y=-2x-3(2)点D在直线l![]() 上,理由见解析(3)13.5
上,理由见解析(3)13.5
【解析】
(1)根据平移的性质得到点C的坐标;把点B、C的坐标代入直线方程y=kx+b(k≠0)来求该直线方程
(2)根据平移的性质得到点D的坐标,然后将其代入(1)中的函数解析式进行验证即可
(3)根据点B的坐标求得直线l![]() 的解析式,据此求得相关线段的长度,并利用三角形的面积公式进行解答
的解析式,据此求得相关线段的长度,并利用三角形的面积公式进行解答
(1)∵B(-3,3),将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,
∴-3+1=-2,3-2=1,
∴C的坐标为(-2,1)
设直线l![]() 的解析式为y=kx+c,
的解析式为y=kx+c,
∵点B,C在直线l![]() 上
上
代入得![]()
解得k=-2,c=-3,
∴直线l![]() 的解析式为y=-2x-3
的解析式为y=-2x-3
(2)∵将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,C(-2,1),
∴-2-3=-5,1+6=7
∴D的坐标为(-5,7)
代入y=-2x-3时,左边=右边,
即点D在直线l![]() 上
上
(3)把B的坐标代入y=x+b得:3=-3+b,
解得:b=6
∴y=x+6,
∴E的坐标为(0,6),
∵直线y=-2x-3与y轴交于A点,
∴A的坐标为(0,-3)
∴AE=6+3=9;
∵B(-3,3)
∴△ABE的面积为![]() ×9×|-3|=13.5
×9×|-3|=13.5


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂将地处A,B两地的两个小工厂合成一个大厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修一条笔直的公路(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一以C点为中心,半径为0.7km的圆形公园,则修筑的这条公路会不会穿过公园?为什么?(提示:判断以点C为圆心的圆与AB的关系)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),已知,∠ACB=90°,AC=BC, AB=26.如果每块砖的厚度相等,砖缝厚度忽略不计,那么砌墙砖块的厚度为( )
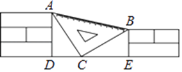
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分別标有数字1、﹣2、3、﹣4,这些卡片除数字外都相同.王兴从口袋中随机抽取一张卡片,钟华从剩余的三张卡片中随机抽取一张,求两张卡片上数字之积.
(1)请你用画树状图或列表的方法,列出两人抽到的数字之积所有可能的结果.
(2)求两人抽到的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】善于学习的小明在学习了一次方程(组),一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点C的坐标为(1,3),那么不等式kx+b≤k1x+b1的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
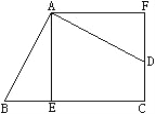
【题目】如图,四边形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,![]() 旋转后能与
旋转后能与![]() 重合.
重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5㎝,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
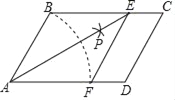
【题目】如图,在ABCD中,以点4为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的长为半径画弧,两弧交于点P;连接AP并廷长交BC于点E,连接EF
BF的长为半径画弧,两弧交于点P;连接AP并廷长交BC于点E,连接EF
(1)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
(2)若AB=2,AE=2![]() ,求∠BAD的大小.
,求∠BAD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知a=3,b和c是关于x的方程x2+mx+2-![]() m=0的两个实数根.
m=0的两个实数根.
(1)求△ABC的周长.
(2)求△ABC的三边均为整数时的外接圆半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com