
分析 (1)根据与x轴有两个不同的交点,可得△≥0,易得n的取值范围;
(2)求得C点坐标,利用三角形的面积公式可得n;
(3)将顶点横坐标用x表示,纵坐标用y表示,可得关于x,y的函数表达式.
解答 解:(1)△=n2-4×$\frac{1}{2}$×($\frac{1}{2}$n2-n+3)>0,
解得:n>3;
(2)由公式AB=$\frac{\sqrt{△}}{|a|}$=2$\sqrt{2n-6}$,
由顶点坐标公式可得C点横坐标x=$-\frac{b}{2a}$=-$\frac{-n}{2×\frac{1}{2}}$=n;
纵坐标y=$\frac{4ac{-b}^{2}}{4a}$=$\frac{4×\frac{1}{2}×(\frac{1}{2}{n}^{2}-n+3)}{4×\frac{1}{2}}$=3-n,
∴C(n,3-n)
∴$\frac{1}{2}$×|3-n|×$2\sqrt{2n-6}$=4,
解得:n=5;
(3)∵顶点坐标(n,3-n)
即:x=n,y=3-n,
∴y=3-x.(n≥3)
点评 本题主要考查了抛物线与x轴的交点及二次函数的性质,关键是熟练掌握:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:填空题
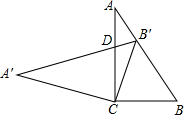 在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.
在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=0.35.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
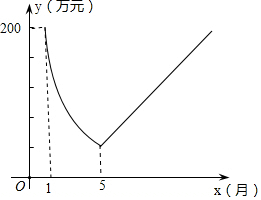 “保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2016年1月的利润为200万元.设2016年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2016年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
“保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2016年1月的利润为200万元.设2016年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2016年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
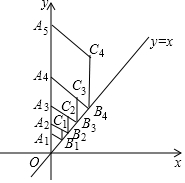 如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].
如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].查看答案和解析>>
科目:初中数学 来源: 题型:解答题
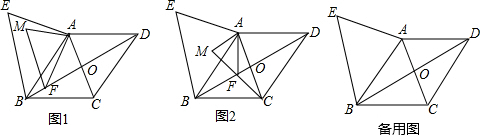
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com