
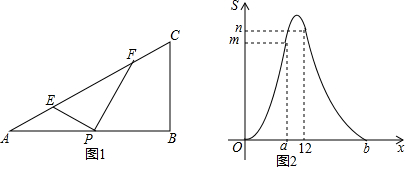
���� ��1���۲�ͼ�ɵó����ۣ�
��2���۲�ͼ��ɵý��ۣ�
��3��С���IJ��������F���C�غ�ʱ����ͼ2��֪��S=m��m��ʾS�����ֵ��
��4������������0��x��8����8��x��12����12��x��24ʱ���ֱ���⼴�ɣ�
��� �⣺��1����ͼ���֪��a=8��
��2���۲�ͼ���֪��P��B�غ�ʱ��x=12��
��3��С���IJ��������F���C�غ�ʱ����ͼ2��֪��S=m��m��ʾS�����ֵ��
��4�������⣬BC=4$\sqrt{3}$��AB=12��
��tan��A=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$��
���A=30�㣬
��EA=EP��
���EAP=��EPA=30�㣬
���FEP=��EAP+��EPA=60�㣬
����ͼ1�У���0��x��8ʱ���ص������ǡ�EPF��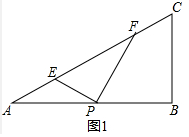
��S=$\frac{1}{2}$•EP•PF=$\frac{1}{2}$•$\frac{\sqrt{3}}{3}$x•x=$\frac{\sqrt{3}}{6}$x2
����ͼ3�У���8��x��12ʱ���ص��������ı���EPMC��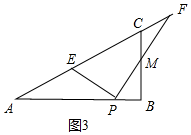
S=S��EPF-S��CFM=$\frac{\sqrt{3}}{6}$x2-$\frac{1}{2}$•$\frac{\sqrt{3}x-8\sqrt{3}}{2}$•2$\sqrt{3}$•$\frac{\sqrt{3}x-8\sqrt{3}}{2}$=-$\frac{7\sqrt{3}}{12}$x2+12$\sqrt{3}$-48$\sqrt{3}$��
�۵�12��x��24ʱ���ص������ǵȱ������Ρ�ECM��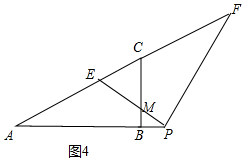
S=$\frac{\sqrt{3}}{4}$•��8$\sqrt{3}$-$\frac{\sqrt{3}}{3}$x��2=$\frac{\sqrt{3}}{12}$x2-4$\sqrt{3}$x+48$\sqrt{3}$��
��������S=.$\left\{\begin{array}{l}{\frac{\sqrt{3}}{6}{x}^{2}}&{��0��x��8��}\\{-\frac{7\sqrt{3}}{12}{x}^{2}+12\sqrt{3}x-48\sqrt{3}}&{��8��x��12��}\\{\frac{\sqrt{3}}{12}{x}^{2}-4\sqrt{3}x+48\sqrt{3}}&{��12��x��24��}\end{array}\right.$��
���� ���⿼�鶯�����⺯��ͼ��30�ȵ�ֱ�������ε����ʡ������ε������֪ʶ������Ĺؼ����������⣬����ͼ����Ϣ�����������ν�ϵ���ѧ˼�룬ѧ���÷ֶκ�����ʾ��������ʽ�������п��������ͣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
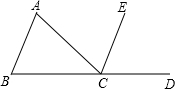 ��ͼ����ABC�У�AC=BC����D��BC���ӳ����ϣ�CE��AB����˵����CE�ǡ�ACD�Ľ�ƽ���ߣ�
��ͼ����ABC�У�AC=BC����D��BC���ӳ����ϣ�CE��AB����˵����CE�ǡ�ACD�Ľ�ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
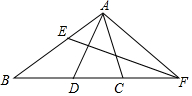 ��ͼ��AD�ǡ�BAC�Ľ�ƽ���ߣ�AD�Ĵ�ֱƽ���߽�AB�ڵ�E����BC�ӳ����ڵ�F��
��ͼ��AD�ǡ�BAC�Ľ�ƽ���ߣ�AD�Ĵ�ֱƽ���߽�AB�ڵ�E����BC�ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǰ�ԲO��ֱ��������AM��BN�ֱ����ԲO�����ڵ�A��B����E�ڰ�Բ�ϣ���D������AM�ϣ�����DE���ӳ�������BN�ڵ�C������AE���ӳ�������BN�ڵ�G��
��ͼ��AB�ǰ�ԲO��ֱ��������AM��BN�ֱ����ԲO�����ڵ�A��B����E�ڰ�Բ�ϣ���D������AM�ϣ�����DE���ӳ�������BN�ڵ�C������AE���ӳ�������BN�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
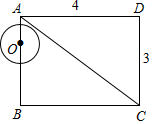 ��ͼ��ʾ����֪����ABCD�У�AB=3��BC=4��O��AB���ϵ�һ�����㣬AO=m���ҡ�O�İ뾶��Ϊ1����
��ͼ��ʾ����֪����ABCD�У�AB=3��BC=4��O��AB���ϵ�һ�����㣬AO=m���ҡ�O�İ뾶��Ϊ1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
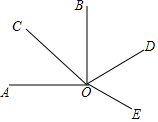 ��ͼ����AOB=90�㣬��BOE=110�㣬OB��OD�ֱ�ƽ�֡�COD����BOE�����AOE����AOC�Ķ�����
��ͼ����AOB=90�㣬��BOE=110�㣬OB��OD�ֱ�ƽ�֡�COD����BOE�����AOE����AOC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com