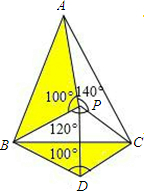
如图所示:
将含有PA、PB边的三角形△BPA,以B为轴心,顺时针方向旋转60°,
则将△BPA移到△BDC,△BDC≌△BPA,BP=BD DC=PA,∠BDC=100°,
因为旋转60°,所以△BDP为等边形,等边三角形,三边相等,三角相等都是60°,
给我们解题极大方便,因为PD=PB,△PDC即由,
PA、PB、PC构成的三角形∠DPC=120°-60°=60°,
∠PDC=100°-60°=40°,
∠DCP=180°-60°-40°=80°,
40:60:80=2:3:4,
(其实这种解题方法思路是十分清晰的,为了把三条分散的射线构成一个三角形,
自然要把PB、PA所在的△PAB,整体移到PC这一边,BA移60°到BC和BC重合,P落到D上.
因为移动60°构成了△PBD为等边形PB=BD=PD,于是△PDC就是PA、PB、PC,构成的三角形,
由于AB=BC,AB与BC重合△ABP≌△BCD,保留了原来已知条件,即BD=BP,DC=PA,
∠BDC=100°移动60°构成的△PBD等边等角,
于是顺理成章的把PB用等长线把PD代替,这样才能构成△PDC,PD=PB,DC=PA,
∴△PDC为PA、PB、PC三条线段构成的三角形.
已知条件∠BPC=120°,仍然保留∠DPC=120°-60°=60°,
∠BDC=100°仍然保留∠PDC=100°-60°=40°,
∠PCD=180°-60°-40°=80°,
(40:60:80=2:3:4.)