
 如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )
如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 设点C的坐标为(m,$\frac{1}{m}$),则点A的坐标为(m,$\frac{k}{m}$),点B的坐标为(km,$\frac{1}{m}$),由此即可得出AC、BC的长度,再根据三角形的面积结合S△ABC=8,即可求出k值,取其正值即可.
解答 解:设点C的坐标为(m,$\frac{1}{m}$),则点A的坐标为(m,$\frac{k}{m}$),点B的坐标为(km,$\frac{1}{m}$),
∴AC=$\frac{k}{m}$-$\frac{1}{m}$=$\frac{k-1}{m}$,BC=km-m=(k-1)m,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$(k-1)2=8,
∴k=5或k=-3.
∵反比例函数y=$\frac{k}{x}$在第一象限有图象,
∴k=5.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征以及三角形的面积,设出点C的坐标,表示出点A、B的坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
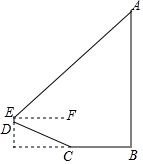 位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)| A. | 22.5 米 | B. | 24.0 米 | C. | 28.0 米 | D. | 33.3 米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165,165 | B. | 165,170 | C. | 170,165 | D. | 170,170 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次数学课上,王老师在黑板上画出图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出∠CAD=∠BDA.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)
在一次数学课上,王老师在黑板上画出图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出∠CAD=∠BDA.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.
如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com