
【题目】“龟、蟹赛跑趣事”:某天,乌龟和螃蟹在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑500米。当螃蟹领先乌龟300米时,螃蟹停下来休息并睡着了,当乌龟追上螃蟹的瞬间,螃蟹惊醒了(惊醒时间忽略不计)并立即以原来的速度继续跑向终点,并赢得了比赛。在比赛的整个过程中,乌龟和螃蟹的距离![]() (米)与乌龟出发的时间
(米)与乌龟出发的时间![]() (分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
(分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
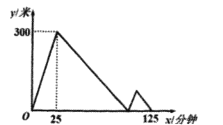
【答案】75
【解析】
根据“速度=路程÷时间”结合函数图象即可算出乌龟的速度,再根据“出发25分钟后螃蟹的路程-乌龟的路程=300”即可求出螃蟹的速度,进而即可求出螃蟹、乌龟会合地离起点的时间,结合总路程及二者的速度即可得出结论.
解:由图形可知:乌龟125分钟到达终点,

∴乌龟的速度为:500÷125=4(米/秒),
设螃蟹的速度为v米/秒,
25v-25×4=300,
v=16,
故螃蟹的速度为16米/秒,
300÷4=75(分),
75+25=100,
∴点P(100,0),
螃蟹惊醒后到达终点的时间为:(500-25×16)÷16=6.25分钟,
则螃蟹到达终点时,乌龟距终点的距离为:4×(125-100-6.25)=75(米).
故答案为:75


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
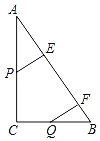
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
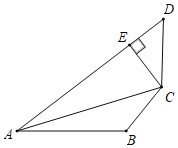
【题目】如图,在四边形ABCD中,CB=CD,∠D+∠ABC=180°,CE⊥AD于E.
(1)求证:AC平分∠DAB;
(2)若AE=3ED=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
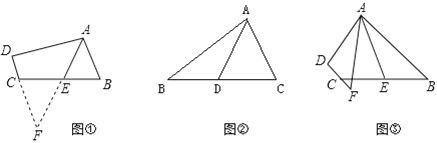
【题目】(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB,AD,DC之间的等量关系______.
(2)同题探究.
①如图②,AD是△ABC的中线,AB=6,AC=4,求AD的范围:
②如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片![]() 放入以
放入以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 边上一点
边上一点![]() 为坐标原点的平面直角坐标系中,连结
为坐标原点的平面直角坐标系中,连结![]() 。将纸片
。将纸片![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,若
处,若![]() ,则点
,则点![]() 的坐标为________________。
的坐标为________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,
,![]() 的解析式为
的解析式为![]() ,
,![]() 的解析式为
的解析式为![]() 且
且![]() ,两直线的交点
,两直线的交点![]() 。
。

(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(Ⅰ)求这个二次函数的解析式;
(Ⅱ)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(Ⅲ)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.
(1)若点P、Q均以3cm/s的速度移动,则:AP= cm;QC= cm.(用含t的代数式表示)
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间PD=PQ,使△DPQ为等腰三角形?
(3)若点P、Q均以3cm/s的速度移动,经过多长时间,四边形BPDQ为菱形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com