

分析 (1)作BS⊥AD于S,ER⊥AD于R,如图1,根据旋转的性质得∠CDE=∠CAB=90°,AB=DE,CA=CD,则根据等腰三角形的性质得∠CAD=∠CDA,再根据等角的余角相等得到∠1=∠2,则可根据“AAS”判定△ABS≌△DER,得到BS=RE,然后证明△BSF≌△ERF得到BF=EF;
(2)根据旋转的性质得CB=CE,CA=CD,∠ACB=∠DCE,根据等腰三角形的性质得CF⊥BE,AT=DT,∠1=∠2=∠3=∠4,则AF:AT=5:3,再根据角平分线定理得CF:CT=FA:AT=5:3,接着通过Rt△ACB∽△Rt△TCF可确定CA:AB:BC=3:4:5,然后利用两组对应边成比例,夹角相等的两三角形相似证明△BAP∽△BCH,得到∠1=∠5,于是判断AN∥BE,则利用平行线分线段成比例定理得到$\frac{AM}{EF}$=$\frac{CM}{CF}$=$\frac{CA}{CE}$=$\frac{3}{5}$,$\frac{CM}{CF}$=$\frac{MN}{BF}$,而BF=EF,所以AM=MN,AM=$\frac{3}{5}$EF,最后利用PM∥BF得到$\frac{PM}{BF}$=$\frac{PH}{BH}$=$\frac{1}{5}$,则AM=3PM,所以MN=3PM,所以NP:AM=2:3.
解答 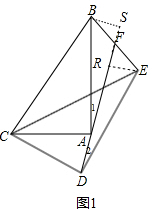 (1)证明:作BS⊥AD于S,ER⊥AD于R,如图1,
(1)证明:作BS⊥AD于S,ER⊥AD于R,如图1,
∵△ABC绕点C顺时针旋转得到△DEC,
∴∠CDE=∠CAB=90°,AB=DE,CA=CD,
∵CA=CD,
∴∠CAD=∠CDA,
∵∠1+∠CAD=90°,∠2+∠CDA=90°,
∴∠1=∠2,
在△ABS和△DER中
$\left\{\begin{array}{l}{∠ASB=∠DRE}\\{∠1=∠2}\\{AB=DE}\end{array}\right.$,
∴△ABS≌△DER,
∴BS=RE,
在△BSF和△ERF中
$\left\{\begin{array}{l}{∠BFS=∠EFR}\\{∠BSF=∠ERF}\\{BS=ER}\end{array}\right.$,
∴△BSF≌△ERF,
∴BF=EF;
(2)解:NP:MA=2:3.理由如下:
∵△ABC绕点C顺时针旋转得到△DEC,
∴CB=CE,CA=CD,∠ACB=∠DCE,
而BF=EF,CT⊥AD,
∴CF⊥BE,AT=DT,∠1=∠2=∠3=∠4,
∵AF:AD=5:6,
∴AF:AT=5:3,
∵CA为△FCT的角平分线,
∴CF:CT=FA:AT=5:3,
∵∠1+∠2=∠2+∠3,即∠BCA=∠FCT,
∴Rt△ACB∽△Rt△TCF,
∴$\frac{BC}{CF}$=$\frac{CA}{CT}$,
即$\frac{BC}{CA}$=$\frac{CF}{CT}$=$\frac{5}{3}$,
∴CA:AB:BC=3:4:5,
∵BP=4PH,
∴BP:BH=3:5,
∴BA:BC=BP:BH,
∵BH平分∠ABC,
∴∠ABP=∠CBH,
∴△BAP∽△BCH,
∴∠1=∠5,
而∠2=∠1,
∴∠2=∠5,
而∠5+∠MAC=90°,
∴∠2+∠MAC=90°,
∴∠AMC=90°,
∴AN∥BE,
∴$\frac{AM}{EF}$=$\frac{CM}{CF}$=$\frac{CA}{CE}$=$\frac{3}{5}$,$\frac{CM}{CF}$=$\frac{MN}{BF}$,
而BF=EF,
∴AM=MN,AM=$\frac{3}{5}$EF,
∵PM∥BF,
∴$\frac{PM}{BF}$=$\frac{PH}{BH}$=$\frac{1}{5}$,
∴AM=3PM,
∴MN=3PM,
∴PN=2PM,
∴NP:AM=2:3.
点评 本题考查了几何变换综合题:熟练掌握旋转的性质、等腰三角形的性质和全等三角形的判定与性质;会根据相似三角形的判定方法证明三角形相似,能运用勾股定理和相似比得到线段之间的关系.解决本题的关键是合理构建全等三角形证明线段相等和找出相似三角形,利用相似比确定NP和AM之间的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
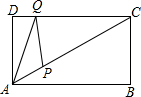 如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是4$\sqrt{3}$.
如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
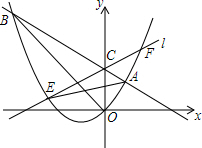 如图,在平面直角坐标系xOy中,直线y=kx+$\frac{8}{5}$与经过原点O的抛物线y=ax2+bx+c交于点A(1,1)和点B(-4,m),与y轴交于点C
如图,在平面直角坐标系xOy中,直线y=kx+$\frac{8}{5}$与经过原点O的抛物线y=ax2+bx+c交于点A(1,1)和点B(-4,m),与y轴交于点C查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com