
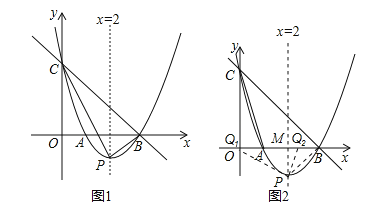
【题目】如图,直线y=﹣x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线![]() 与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
(1)求该抛物线的解析式;
(2)连接PB、PC,求△PBC的面积;
(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)3;(3)存在两点Q1(0,0),Q2(
;(2)3;(3)存在两点Q1(0,0),Q2(![]() ,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
【解析】
试题分析:(1)根据二次函数的对称性,已知对称轴的解析式以及B点的坐标,即可求出A的坐标,利用抛物线过A、B、C三点,可用待定系数法来求函数的解析式
(2)首先利用各点坐标得出得出△PBC是直角三角形,进而得出答案;
(3)本题要先根据抛物线的解析式求出顶点P的坐标,然后求出BP的长,进而分情况进行讨论:
①当![]() ,∠PBQ=∠ABC=45°时,根据A、B的坐标可求出AB的长,根据B、C的坐标可求出BC的长,已经求出了PB的长度,那么可根据比例关系式得出BQ的长,即可得出Q的坐标.
,∠PBQ=∠ABC=45°时,根据A、B的坐标可求出AB的长,根据B、C的坐标可求出BC的长,已经求出了PB的长度,那么可根据比例关系式得出BQ的长,即可得出Q的坐标.
②当![]() ,∠QBP=∠ABC=45°时,可参照①的方法求出Q的坐标.
,∠QBP=∠ABC=45°时,可参照①的方法求出Q的坐标.
③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
试题解析:(1)∵直线y=﹣x+3与x轴相交于点B,∴当y=0时,x=3,∴点B的坐标为(3,0),∵y=﹣x+3过点C,易知C(0,3),∴c=3.
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,根据抛物线的对称性,∴点A的坐标为(1,0).
又∵抛物线![]() 过点A(1,0),B(3,0),∴
过点A(1,0),B(3,0),∴![]() ,解得:
,解得:![]() ,∴该抛物线的解析式为:
,∴该抛物线的解析式为:![]() ;
;
(2)如图1,∵![]() =
=![]() ,又∵B(3,0),C(0,3),∴PC=
,又∵B(3,0),C(0,3),∴PC=![]() =
=![]() =
=![]() ,PB=
,PB=![]() =
=![]() ,∴BC=
,∴BC=![]() =
=![]() =
=![]() ,又∵
,又∵![]() =2+18=20,
=2+18=20,![]() =20,∴
=20,∴![]() ,∴△PBC是直角三角形,∠PBC=90°,∴S△PBC=
,∴△PBC是直角三角形,∠PBC=90°,∴S△PBC=![]() PBBC=
PBBC=![]() =3;
=3;
(3)如图2,由![]() =
=![]() ,得P(2,﹣1),设抛物线的对称轴交x轴于点M,∵在Rt△PBM中,PM=MB=1,∴∠PBM=45°,PB=
,得P(2,﹣1),设抛物线的对称轴交x轴于点M,∵在Rt△PBM中,PM=MB=1,∴∠PBM=45°,PB=![]() .
.
由点B(3,0),C(0,3)易得OB=OC=3,在等腰直角三角形OBC中,∠ABC=45°,由勾股定理,得BC=![]() .
.
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当![]() ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即![]() ,解得:BQ=3,又∵BO=3,∴点Q与点O重合,∴Q1的坐标是(0,0).
,解得:BQ=3,又∵BO=3,∴点Q与点O重合,∴Q1的坐标是(0,0).
②当![]() ,∠QBP=∠ABC=45°时,△QBP∽△ABC.
,∠QBP=∠ABC=45°时,△QBP∽△ABC.
即![]() ,解得:QB=
,解得:QB=![]() .
.
∵OB=3,∴OQ=OB﹣QB=3﹣![]() =
=![]() ,∴Q2的坐标是(
,∴Q2的坐标是(![]() ,0).
,0).
③当Q在B点右侧,则∠PBQ=180°﹣45°=135°,∠BAC<135°,故∠PBQ≠∠BAC.
则点Q不可能在B点右侧的x轴上.
综上所述,在x轴上存在两点Q1(0,0),Q2(![]() ,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.


科目:初中数学 来源: 题型:
【题目】已知n棱柱中的棱长都是15 cm,且该棱柱共有16个顶点.
(1)该棱柱的底面是______边形;
(2)求该棱柱所有棱长的和;
(3)求该棱柱侧面展开图的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣a)(x﹣b)﹣2,(a<b)的图象与x轴交点的横坐标为m,n,且m<n,则a,b,m,n的大小关系是( )
A. m<a<b<n B. a<m<b<n C. a<m<n<b D. m<a<n<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)2(x2-2x+5)-3(2x2-5)=________________.
(2)4(m-3n)-5(3n-10m)-13(n-2m)=_________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com