
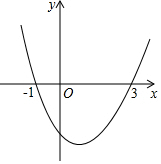
 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(-1,0),(3,0)两点,下列说法正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(-1,0),(3,0)两点,下列说法正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据抛物线与x轴的交点及对称性可得结论;
②由图象得结论;
③将x=-1和x=3代入得两式,相加可得:3a+c=0,由a>0,可得结论;
④根据抛物线的增减性可得结论.
解答 解:①∵抛物线与x轴交于(-1,0),(3,0),
∴抛物线的对称轴是:x=$\frac{-1+3}{2}$=1,
∴-$\frac{b}{2a}$=1,
2a+b=0,
故①正确;
②由图可知:当-1≤x≤3时,y≤0;
故②不正确;
③由题意得:a-b+c=0①,9a+3b+c=0②
①×3+②得:3a+c=0,
∵抛物线开口向上,
∴a>0,
∴4a+c>0,
故③正确;
④分三种情况:
i)若(x1,y1),(x2,y2)是抛物线上对称轴左侧上的两点,则当x1<x2时,y1>y2;
ii)若(x1,y1),(x2,y2)是抛物线上对称轴右侧上的两点,则当x1<x2时,y1<y2;
iii)若(x1,y1),(x2,y2)是抛物线上对称轴两侧上的两点,则当x1<x2时,y1>与y2的大小不确定;
故④不正确;
所以本题正确的有:①③,2个;
故选B.
点评 本题考查了二次函数与系数的关系、抛物线与x轴的交点及二次函数的性质,熟练掌握二次函数的性质是关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
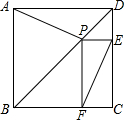 如图,P是正方形ABCD对角线BD上的一动点(不与B、D重合),PE⊥DC,PF⊥BC,E、F分别为垂足.
如图,P是正方形ABCD对角线BD上的一动点(不与B、D重合),PE⊥DC,PF⊥BC,E、F分别为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
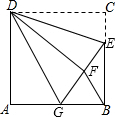 如图,正方形ABCD的边长为12,点E在边BC上,且BE=2CE.将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连结DG,BF.下列结论:①△DAG≌△DFG;②DG∥BF;③EG=10;④S△BEF=9.6.其中所有正确结论的序号是①②③④(填序号)
如图,正方形ABCD的边长为12,点E在边BC上,且BE=2CE.将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连结DG,BF.下列结论:①△DAG≌△DFG;②DG∥BF;③EG=10;④S△BEF=9.6.其中所有正确结论的序号是①②③④(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com