
【题目】阅读理解:若一个三位数是312,则百位上数字为3,十位上数字为1,个位上数字为2,这个三位数可表示为3×100+1×10+2;若一个三位数是﹣312,则百位上数字为3,十位上数字为1,个位上数字为2,这个三位数可表示为﹣(3×100+1×10+2);
应用:有一个正的四位数,千位上数字为a,百位上数字为b,十位上数字为c,个位数字为d,且a>d,b﹣c>1.按顺序完成一下运算;
第一步:交换千位和个位上的数字也交换百位和十位上的数字,而构成另一个四位数;
第二步:用原四位数减去第一步构成的四位数,把这个新四位数记为M;
第三步:交换M的百位和十位上的数字,又构成一个新四位数,记为N;
第四部,将M和N相加
(1)第一步构成的另一个四位数可表示为 ;
(2)试判断M百位和十位的数字之和是否为定值?请说明理由.
(3)若M和N相加的值为8892,求a﹣d的值.
【答案】(1)1000d+100c+10b+a;(2)定值为8,见解析;(3)8892
【解析】
(1)根据题意表示出另一个四位数即可;
(2)定值为8,根据题意确定出M十位与百位数字,相加即可作出判断;
(3)根据题意确定出a﹣d的值即可.
(1)根据题意得:1000d+100c+10b+a;
故答案为:1000d+100c+10b+a;
(2)定值为8,
M的十位数字为:![]() ×[10(c﹣1)+100﹣10b]=c﹣b﹣1+10,M百位数字为:
×[10(c﹣1)+100﹣10b]=c﹣b﹣1+10,M百位数字为:![]() × [100(b﹣1)﹣100c]=b﹣1﹣c,
× [100(b﹣1)﹣100c]=b﹣1﹣c,
∴c﹣b﹣1+10+b﹣1﹣c=8,
则定值为8;
(3)依题意得:∵交换M的百位和十位上的数字,又构成一个新四位数,记为N
∴M的千位、N的千位相同,M的个位、N的个位相同
∵M和N相加的值为8892
∴M的千位、N的千位为4,M的个位、N的个位为6,
∴a﹣d=4,例如5861﹣1685=4167;4716+4176=8892.


科目:初中数学 来源: 题型:
【题目】已知:OB、OC、OE是∠AOD内的射线,若∠AOD=130°.
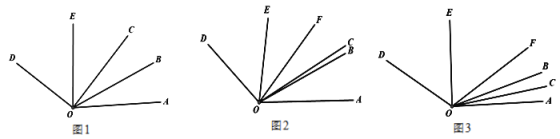
(1)如图1,OB是∠AOC的平分线,OE是∠COD的平分线,∠BOE=_____度;
(2)OF也是∠AOD内的射线,如图2,若∠FOC=20°,OB平分∠AOF,OE平分∠COD,当射线OC绕点O在∠AOF内旋转时,求∠BOE的大小;
(3)在(2)的条件下,当射线OC从边OA开始绕O点以每秒2°的速度逆时针旋转t秒,如图3,若∠AOB:∠DOE=2:3,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.
(1)如果小张家一个月用电128度,那么这个月应缴纳电费多少元?
(2)如果小张家一个月用电a度![]() ,那么这个月应缴纳电费多少元?(用含a的代数式表示)
,那么这个月应缴纳电费多少元?(用含a的代数式表示)
(3)如果这个月缴纳电费为147.8元,那么小张家这个月用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
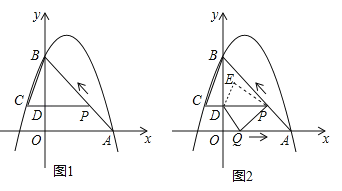
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知圆锥底面半径r=10cm,母线长为40cm.

(1)求它的侧面展开图的圆心角和表面积.
(2)若一只甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点![]() 和点
和点![]() 处各折一下,得到一条“折线数轴”,图中点
处各折一下,得到一条“折线数轴”,图中点![]() 表示-12,点
表示-12,点![]() 表示10,点
表示10,点![]() 表示20,我们称点
表示20,我们称点![]() 和点
和点![]() 在数轴上相距32个长度单位.动点
在数轴上相距32个长度单位.动点![]() 从点
从点![]() 出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点
出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点![]() 运动到点
运动到点![]() 期间速度变为原来的一半,之后立刻恢复原速;同时,动点
期间速度变为原来的一半,之后立刻恢复原速;同时,动点![]() 从点
从点![]() 出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点
出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点![]() 运动到点
运动到点![]() 期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为
期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为![]() 秒.则:
秒.则:
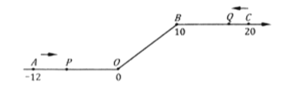
(1)动点![]() 从点
从点![]() 运动至点
运动至点![]() 需要时间多少秒?
需要时间多少秒?
(2)若![]() ,
,![]() 两点在点
两点在点![]() 处相遇,则点
处相遇,则点![]() 在折线数轴上所表示的数是多少?
在折线数轴上所表示的数是多少?
(3)求当![]() 为何值时,
为何值时,![]() 、
、![]() 两点在数轴上相距的长度与
两点在数轴上相距的长度与![]() 、
、![]() 两点在数轴上相距的长度相等.
两点在数轴上相距的长度相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com