
分析 (1)设甲种材料每千克x元,乙种材料每千克y元,根据“购买价格=甲材料单价×数量+乙材料单价×数量”列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设生产B产品a件,生产A产品(80-a)件.根据“购买材料钱=生产A产品的件数×A产品所需材料钱+生产B产品的件数×B产品所需材料钱”结合购买资金不能超过17000元得出关于a的一元一次不等式,解不等式即可得出结论;
(3)设生产成本为W元,根据数量关系寻找出W关于a的函数关系式,由一次函数的单调性即可得出结论.
解答 解:(1)设甲种材料每千克x元,乙种材料每千克y元,
依题意得:$\left\{\begin{array}{l}x+y=80\\ 2x+3y=205\end{array}\right.$,解得:$\left\{\begin{array}{l}x=35\\ y=45\end{array}\right.$.
答:甲种材料每千克35元,乙种材料每千克45元.
(2)设生产B产品a件,生产A产品(80-a)件.
依题意得:(35×4+45×1)(80-a)+(45×3+35×3)a≤17000,解得:a≤40.
又∵a≥37,
∴37≤a≤40.
∵a的值为非负整数,
∴a=37、38、39、40;
答:共有如下四种方案:
| A(件) | 43 | 42 | 41 | 40 |
| B(件) | 37 | 38 | 39 | 40 |
点评 本题考查了一次函数的应用,解二元一次方程组以及解一元一次不等式,解题的关键是:(1)根据数量关系找出二元一次方程组;(2)根据数量关系列出一元一次不等式;(3)根据数量关系找出W关于a的函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系得出方程(方程组、或不等式)是关键.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:选择题
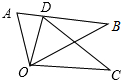 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数为( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数为( )| A. | 36° | B. | 38° | C. | 34° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
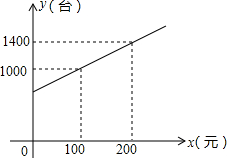 为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=-$\frac{1}{5}$x+110(x≥0).
为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=-$\frac{1}{5}$x+110(x≥0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
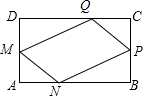 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1;
(1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com