练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
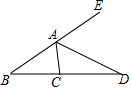
    12．AD是∠CAE的平分线，∠B=35°，∠DAE=60°，则∠ACD=（　　）
    A．25°B．60°C．85°D．95°

    分析 根据角平分线的定义得到∠EAC=2∠DAE=120°，根据三角形的外角的性质计算即可．

    解答 解：∵AD是∠CAE的平分线，
    ∴∠EAC=2∠DAE=120°，
    ∴∠ACD=∠EAC-∠B=85°，
    故选：C．

    点评 本题考查的是三角形的外角的性质、角平分线的定义，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

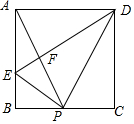    2．如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（　　）
    A．当P为BC中点，△APD是等边三角形B．当△ADE∽△BPE时，P为BC中点
    C．当AE=2BE时，AP⊥DED．当△APD是等边三角形时，BE+CD=DE

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．平面直角坐标系xOy中，点A、B分别在函数y1=$\frac{3}{x}$（x＞0）与y2=-$\frac{3}{x}$（x＜0）的图象上，A、B的横坐标分别为a、b．
    （1）若AB∥x轴，求△OAB的面积；
    （2）若△OAB是以AB为底边的等腰三角形，且a+b≠0，求ab的值；
    （3）作边长为2的正方形ACDE，使AC∥x轴，点D在点A的左上方，那么，对大于或等于3的任意实数a，CD边与函数y1=$\frac{3}{x}$（x＞0）的图象都有交点，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

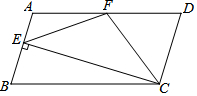    20．如图，在?ABCD中，AD=2AB，F是AD的中点，作CE⊥AB于E，在线段
    AB上，连接EF、CF．则下列结论：①∠BCD=2∠DCF；②∠ECF=∠CEF；③S△BEC=2S△CEF；④∠DFE=3∠AEF，其中一定正确的是（　　）
    A．②④B．①②④C．①②③④D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

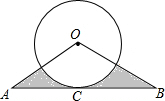    7．如图，在△ABC中，OA=OB=6，∠O=120°，以点O为圆心的⊙O和底边AB相切于点C，则阴影部分的面积为9$\sqrt{3}$-3π．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图1，在正方形ABCD中，O是对角线AC上一点，点E在BC的延长线上，且OE=OB．
    （1）求证：△OBC≌△ODC．
    （2）求证：∠DOE=∠ABC．
    （3）把正方形ABCD改为菱形，其他条件不变（如图2），若∠ABC=52°，求∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知二次函数 y=kx2-（4k+1）x+4（k≠0）．
    （1）若该二次函数的顶点在x轴上，求k的值；
    （2）若x＜-1时，y随x的增大而增大，求实数k的取值范囤；
    （3）①说明点B（4，0）在抛物线y=kx2-（4k+1）x+4上；
               ②直线x=1与抛物线交于点E，与x轴交于点F，且45°≤∠EBF≤60°，求实数k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．从边长为a的正方形剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
    （1）上述操作能验证的等式是B（请选择正确的一个）
    A．a2-2ab+b2=（a-b）2
    B．a2-b2=（a+b）（a-b）
    C．a2+ab=a（a+b）
    （2）若x2-9y2=12，x+3y=4，求x-3y的值；
    （3）计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{{2016}^{2}}$）（1-$\frac{1}{{2017}^{2}}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化简（$\frac{{x}^{2}-6x}{x+2}$+2）÷$\frac{{x}^{2}-4}{{x}^{2}+4x+4}$，然后从2、-2、1、-1中选取一个你认为合适的数作为x的值代入求值．

    查看答案和解析>>

    同步练习册答案