
【题目】已知△ABC是等边三角形,点P是平面内一点,且四边形PBCD为平行四边形,将线段CD绕点C逆时针旋转60°,得到线段CF
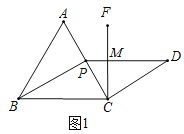
(1)如图1,当P为AC的中点时,求证:FC⊥PD.
(2)如图2,当P为△ABC内任一点时,连接PA、PF、AF,试判断△PAF的形状,并证明你的结论.
(3)当B、P、F三点共线且AB=![]() ,PB=3时,求PA的长.
,PB=3时,求PA的长.

【答案】(1)见解析;(2)△PAF是等边三角形,证明见解析;(3)PA的长为2或5.
【解析】
(1)如图1,利用等边三角形和平行四边形的性质求得∠FCD+∠D=90°即得结论;
(2)△PAF是等边三角形.如图2,延长BC,先利用等边三角形的性质和平行四边形的性质证得∠2=∠4,再根据SAS证明△ABP≌△ACF,进一步根据等边三角形的判定定理即可证得结论;
(3)需要分类讨论:当点P在线段BF上和当点P落在线段FB的延长线上两种情况,通过作辅助线,构造直角三角形,再结合勾股定理即可求出结果.
(1)证明:如图1,设FC、PD交于点M,
∵△ABC是等边三角形,P为AC的中点,
∴∠PBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∵四边形PBCD为平行四边形,
∴∠D=∠PBC=30°.
∵∠FCD=60°,
∴∠FCD+∠D=90°,
∴∠CMD=90°,
∴FC⊥PD;
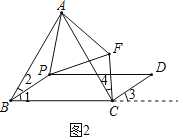
(2)△PAF是等边三角形,理由如下:
如图2,延长BC,∵△ABC为等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∴∠2=60°﹣∠1,∠4=180°﹣60°﹣60°﹣∠3=60°﹣∠3.
∵四边形PBCD是平行四边形,
∴PB∥CD,PB=CD=FC.
∴∠1=∠3,∴∠2=∠4.
又AB=AC,PB=FC,
∴△ABP≌△ACF(SAS).
∴AP=AF,∠BAP=∠CAF.
∵∠BAP+∠PAC=60°,
∴∠PAC+∠CAF=∠PAF=60°,
∴△PAF是等边三角形;
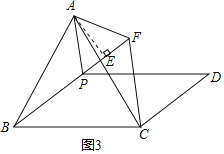
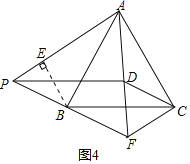
(3)①当点P在线段BF上时,如图3,过A作AE⊥BF于E,由(2)可得∠APF=60°,
设PE=x,则AE=![]() x,
x,
于是在Rt△ABE中,根据勾股定理得:![]() ,
,
解得:x1=1,x2=![]() (不合题意,舍去)
(不合题意,舍去)
∴PA=2x=2;
②当点P落在线段FB的延长线上时,如图4,过B作BE⊥PA于E,
则在Rt△PBE中,PB=3,由(2)可得∠BPE=60°,∴∠PBE=30°.
∴PE=![]() ,BE=
,BE=![]() .
.
在Rt△ABE中,AB=![]() ,BE=
,BE=![]() ,∴AE=
,∴AE=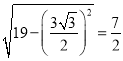 ,
,
∴PA=PE+AE=5.
由于P点不可能在线段BF的延长线上,所以, PA的长为2或5.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查
B. 甲、乙两人跳远成绩的方差分别为![]() ,
,![]() ,说明乙的跳远成绩比甲稳定
,说明乙的跳远成绩比甲稳定
C. 一组数据2,2,3,4的众数是2,中位数是2.5
D. 可能性是1%的事件在一次试验中一定不会发生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数y=﹣x+6图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(1)所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图(2)所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
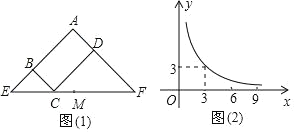
A.当x=3时,EC<EM
B.当y=9时,EC>EM
C.当x增大时,ECCF的值增大
D.当x变化时,四边形BCDA的面积不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,平行四边形ACDE的一边在直径AB上,点E在⊙O上.
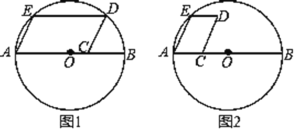
(1)如图1,当点D在⊙O上时,请你仅用无刻度的直尺在AB上取点P,使DP⊥AB于P;
(2)如图2,当点D在⊙O内时,请你仅用无刻度的直尺在AB上取点Q,使EQ⊥AB于Q.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某学校为了了解九年级学生的体能情况,抽取了部分学生进行了体能测试,学生的测试成绩分四类:A:优秀;B:良好;C:合格;D不合格,将抽测学生的成绩绘制成如下两幅不完整的统计图,请根据统计图解答下列问题:
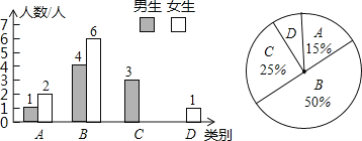
(1)求本次调查的学生总人数;
(2)成绩为C的女生有______人,成绩为D的男生有______人;
(3)扇形统计图中成绩为D的学生所对应的扇形的圆心角度数为______;
(4)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
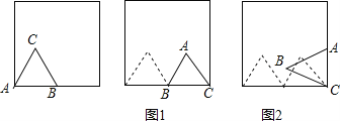
【题目】如图,边长为1的正三角形ABC放置在边长为2的正方形内部,顶点A在正方形的一个顶点上,边AB在正方形的一边上,将△ABC绕点B顺时针旋转,当点C落在正方形的边上时,完成第1次无滑动滚动(如图1);再将△ABC绕点C顺时针旋转,当点A落在正方形的边上时,完成第2次无滑动滚动(如图2),…,每次旋转的角度都不大于120°,依次这样操作下去,当完成第2016次无滑动滚动时,点A经过的路径总长为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
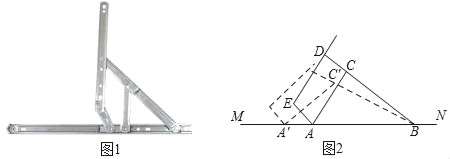
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
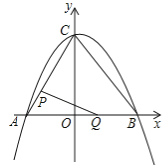
【题目】如图①,在平面直角坐标系中,二次函数y=![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com