
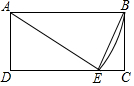
 如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.
如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3. 分析 根据圆的性质得出AE=AB=10,得出∠ABE=∠AEB,由矩形的性质得出∠D=∠C=90°,AB∥CD,CD=AB=10,由平行线的性质得出∠ABE=∠CEB,由勾股定理得出DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=8,证出∠AEB=∠CEB,CE=CD-DE=2,tan∠AEB=tan∠CEB,即可得出答案.
解答 解:根据题意得:AE=AB=10,
∴∠ABE=∠AEB,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,AB∥CD,CD=AB=10,
∴∠ABE=∠CEB,DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=8,
∴∠AEB=∠CEB,CE=CD-DE=2,
∴tan∠AEB=tan∠CEB=$\frac{BC}{CE}$=$\frac{6}{2}$=3;
故答案为:3.
点评 本题考查了矩形的性质、等腰三角形的性质、平行线的性质、勾股定理、三角函数等知识;熟练掌握矩形的性质和勾股定理是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
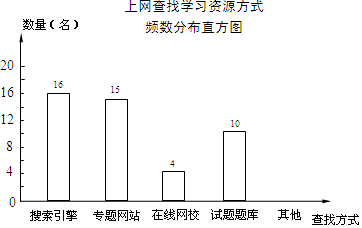 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.| 查找方式 | 频数 | 频率 |
| 搜索引擎 | 16 | 32% |
| 专题网站 | 15 | a |
| 在线网校 | 4 | 8% |
| 试题题库 | 10 | 20% |
| 其他 | b | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
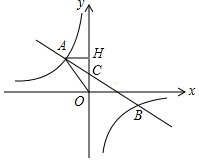 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
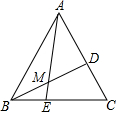 如图,在等边△ABC中,D为AC边上的一点,连接BD,M为BD上一点,且∠AMD=60°,AM交BC于E.当M为BD中点时,$\frac{CD}{AD}$的值为( )
如图,在等边△ABC中,D为AC边上的一点,连接BD,M为BD上一点,且∠AMD=60°,AM交BC于E.当M为BD中点时,$\frac{CD}{AD}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com