
【题目】如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )

A. 若BG∥CH,则四边形BHCG为矩形
B. 若BE=CE时,四边形BHCG为矩形
C. 若HE=CE,则四边形BHCG为平行四边形
D. 若CH=3,CG=4,则CE=2.5
【答案】C
【解析】
由∠ACB角平分线和它的外角的平分线分别交DE于点G和H可得∠HCG=90°,∠ECG=∠ACG即可得HE=EC=EG,再根据A,B,C,D的条件,进行判断.
解:∵∠ACB角平分线和它的外角的平分线分别交DE于点G和H,
∴∠HCG=90°,∠ECG=∠ACG;
∵DE∥AC.
∴∠ACG=∠HGC=∠ECG.
∴EC=EG;
同理:HE=EC,
∴HE=EC=EG=![]() HG;
HG;
若CH∥BG,
∴∠HCG=∠BGC=90°,
∴∠EGB=∠EBG,
∴BE=EG,
∴BE=EG=HE=EC,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形;
故A正确;
若BE=CE,
∴BE=CE=HE=EG,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形,
故B正确;
若HE=EC,则不可以证明则四边形BHCG为平行四边形,
故C错误;
若CH=3,CG=4,根据勾股定理可得HG=5,
∴CE=2.5,
故D正确.
故选:C.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若![]() ,则x为_________.
,则x为_________.
(4)已知x、y满足方程组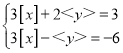
![]() ,求x、y的取值范围.
,求x、y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了某校七年级学生对![]() 《最强大脑》、
《最强大脑》、![]() 《朗读者》、
《朗读者》、![]() 《中国诗词大会》、
《中国诗词大会》、![]() 《极限挑战》四个电视节目的喜爱情况,随机抽取了
《极限挑战》四个电视节目的喜爱情况,随机抽取了![]() 位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
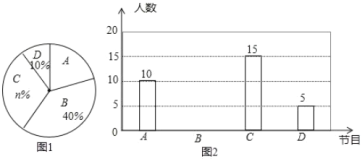
根据统计图提供的信息,回答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在图1中,喜爱《朗读者》节目所对应的扇形的圆心角度数是______度;
(3)请根据以上信息直接在答题卡中补全图2的条形统计图;
(4)已知该校七年级共有420位学生,那么他们最喜欢《中国诗词大会》这个节目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足部分记为负数。评分记录如下:+15,+20,5,4,3,+4,+6,+2,+3,+5,+7,8.
(1)这12名同学中最高分和最低分各是多少?
(2)这些同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,(1)abc>0;(2)4a+2b+c>0;(3)4ac﹣b2<16a;(4)![]() <a<
<a<![]() ;(5)b<c,其中正确的结论有( )
;(5)b<c,其中正确的结论有( )
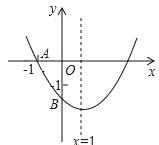
A. (2)(3)(4)(5) B. (1)(3)(4)(5) C. (1)(3)(4) D. (1)(2)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.
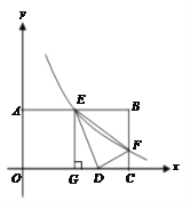
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com