
��1����ͬѧ����ѧ��Σ����ýdz�ƽ��һ���ǣ���ͼ��ʾ������������� ������
������
����AOB��һ������ǣ����dzߵ�ֱ�Ƕ���P��������OA��OB֮�䣬�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M��N�غϣ���PM=PN�����dz߶���P������OP���ǡ�AOB��ƽ���ߣ�
����AOB��һ������ǣ��ڱ�OA��OB�Ϸֱ�ȡOM=ON�����dzߵ�ֱ�Ƕ���P ��������OA��OB֮�䣬�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M��N�غϣ���PM=PN�����dz߶���P������OP���ǡ�AOB��ƽ���ߣ�
��������OA��OB֮�䣬�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M��N�غϣ���PM=PN�����dz߶���P������OP���ǡ�AOB��ƽ���ߣ�
��1�������������������Ƿ���У������У���֤�����������У���˵�����ɣ�
��2���ڷ�������PM=PN������£������ƶ��dzߣ�ͬʱʹPM��OA��PN��OB���˷����Ƿ���У���˵�����ɣ�
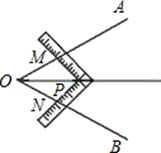
�⣺��1�������������У�ȱ��֤��������ȫ�ȵ�������
��ֻ��OP=OP��PM=PN�����жϡ�OPM�ա�OPN��
��Ͳ����ж�OP���ǡ�AOB��ƽ�� �ߣ�
�ߣ�
����������
֤�����ڡ�OPM�͡�OPN�У�
 ��
��
���OPM�ա�OPN��SSS����
���AOP=��BOP��ȫ�������ζ�Ӧ����ȣ���
��OP���ǡ�AOB��ƽ���ߣ�
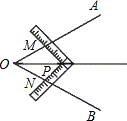
��2������AOB��ֱ��ʱ���˷������У�
���ı����ڽǺ�Ϊ360�㣬��OMP=��ONP=90�㣬��MPN=90�㣬
���AOB=90�㣬
��PM=PN��
��OPΪ��AOB��ƽ���ߣ����������߾�����ȵĵ�������ǵĽ�ƽ�����ϣ���
����AOB��Ϊֱ��ʱ ���˷��������У�
���˷��������У�
��Ϊ��AOB��Ϊ90�㣬�������90�㣬�����ҵ�ͬʱʹPM��OA��PN��OB�ĵ�P��λ�ã�


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д� ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
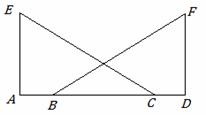
��֪����ͼ����A��B��C��D��ͬһ��ֱ���ϣ�EA��AD��FD��AD��AE=DF��AB=DC��
��֤����ACE=��DBF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
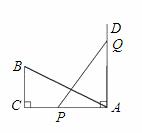
��ͼ��Rt��ABC�У���C=90�㣬AC=8��BC=4��PQ=AB����P���Q�ֱ���AC��AC�Ĵ���AD���ƶ�����AP=_______ʱ����ABC�ա�APQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����M�ڡ�ABC�ڣ�ME��AB��E�㣬MF��BC��F�㣬��ME=MF����ABC=70�㣬���BME=�� ���㣮
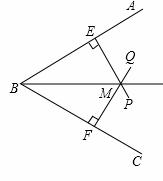
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��OPƽ�� ��
��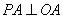 ��
��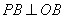 ������ֱ�ΪA��B�����н����в�һ���������ǣ� ��
������ֱ�ΪA��B�����н����в�һ���������ǣ� ��
A.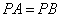 B.
B.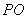 ƽ��
ƽ��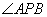 C.
C.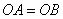 D.
D.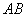 ��ֱƽ��
��ֱƽ��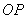
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����Rt��ABC�У���A=90�㣬��ABC��ƽ����BD��AC�ڵ�D��AD=3��BC=10�����BDC��������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
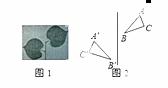
��һ��ͼ��������һ��ֱ�߽�����ԳƱ任��������������ֱ��ƽ�еķ���ƽ�ƣ����ǰ�������ͼ�α任���������ԳƱ任������Ȼ����ճ������У������ش�������ͼ�α任����ͼ1���������ԳƱ任��ƽ�Ʊ任���й����ʣ�����Ϊ�ڻ����ԳƱ任�����У�������Ӧ�����Σ���ͼ2���Ķ�Ӧ�������е������ǣ�������
| �� | A�� | ��Ӧ��������Գ��ᴹֱ | B�� | ��Ӧ�����߱��Գ���ƽ�� |
| �� | C�� | ��Ӧ�����߱��Գ��ᴹֱƽ�� | D�� | ��Ӧ��������ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�㣨3��2������x��ĶԳƵ�Ϊ��������
| �� | A�� | ��3����2 | B�� | ����3��2�� | C�� | ����3����2�� | D�� | ��2����3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com