练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，点D，E，F在边BC上，点P在线段AD上，若PE∥AB，∠PFD=∠C，点D到AB和AC的距离相等．求证：点D到PE和PF的距离相等．

    【答案】证明见解析

    【解析】

    首先由∠PFD＝∠C推出PF∥AC，根据两直线平行，同位角相等，即可求得∠EPD＝∠BAD，∠DPF＝∠CAD，又由点D到AB和AC的距离相等，证得AD是∠BAC的平分线，即可证得DP平分∠EPF，根据角平分线的性质，即可证得结论．

    ∵∠PFD＝∠C，∴PF∥AC，∴∠DPF＝∠DAC．

    ∵PE∥AB，∴∠EPD＝∠BAD．

    ∵点D到AB和AC的距离相等，∴AD是∠BAC的角平分线，∴∠BAD＝∠DAC，∴∠EPD＝∠FPD，即DP平分∠EPF，∴点D到PE和PF的距离相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

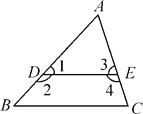
    【题目】如图，(1)∠2与∠B是什么角？若∠1＝∠B，则∠2与∠B有何数量关系？请说明理由．

    (2)∠3与∠C是什么角？若∠4＋∠C＝180°，则∠3与∠C有何数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD的对角线交于点E，有AE=EC，BE=ED，以AB为直径的半圆过点E，圆心为O．
    （1）利用图1，求证：四边形ABCD是菱形．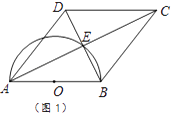
    （2）如图2，若CD的延长线与半圆相切于点F，已知直径AB=8． ①连结OE，求△OBE的面积．
    ②求弧AE的长．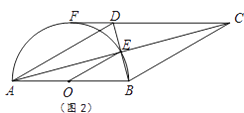

    查看答案和解析>>

    科目：初中数学 来源： 题型：

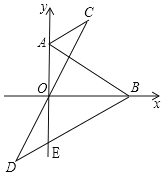
    【题目】在平面直角坐标系中，点A（0，6），B（8，0），AB=10，如图作∠DBO=∠ABO，∠CAy=∠BAO，BD交y轴于点E，直线DO交AC于点C．

    （1）①求证：△ACO≌△EDO；②求出线段AC、BD的位置关系和数量关系；

    （2）动点P从A出发，沿A﹣O﹣B路线运动，速度为1，到B点处停止运动；动点Q从B出发，沿B﹣O﹣A运动，速度为2，到A点处停止运动．二者同时开始运动，都要到达相应的终点才能停止．在某时刻，作PE⊥CD于点E，QF⊥CD于点F．问两动点运动多长时间时△OPE与△OQF全等？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（　　）

    A. 角的内部到角的两边的距离相等的点在角的平分线上

    B. 角平分线上的点到这个角两边的距离相等

    C. 三角形三条角平分线的交点到三条边的距离相等

    D. 三角形三条垂直平分线的交点到三个定点的距离相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如果两个等腰三角形的顶角互补，顶角的顶点又是同一个点，而且它们的腰也分别相等，则称这两个三角形互为“顶补等腰三角形”．

    （1）如图1，若△ABC与△ADE互为“顶补等腰三角形”．∠BAC＞90°，AM⊥BC于M，AN⊥ED于N．求证：DE=2AM；

    （2）如图2，在四边形ABCD中，AD=AB，CD=BC，∠B=90°，∠A=60°，在四边形ABCD的内部是否存在点P，使得△PAD与△PBC互为“顶补等腰三角形”？若存在，请给予证明，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图, 已知∠1＋∠2＝180o, ∠3＝∠B, 试说明∠DEC＋∠C＝180o. 请完成下列填空：

    解：∵∠1＋∠2＝180o（已知）

    又∵∠1＋ ＝180o（平角定义）

    ∴∠2＝ （同角的补角相等）

    ∴ （内错角相等，两直线平行）

    ∴∠3 ＝ （两直线平行，内错角相等）

    又∵∠3＝∠B（已知）

    ∴ （等量代换）

    ∴ ∥ （ ）

    ∴∠DEC＋∠C＝180o（ ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于(　　).

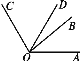
    A. 50° B. 40° C. 30° D. 20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m.
    （结果精确到0.1m。参考数据：tan20°≈0.36,tan18°≈0.32）

    （1）求∠BCD的度数.
    （2）求教学楼的高BD

    查看答案和解析>>

    同步练习册答案