
 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据折叠得出∠C′EF=∠CEF,∠EFD=∠EFD′,根据平行线的性质求出∠EFB=∠C′EF=32°,再逐个判断即可.
解答 解:∵AE∥BG,∠EFB=32°,
∴∠C′EF=∠EFB=32°,
根据折叠得:∠CEF=∠C′EF=32°,∴①正确;
∵AE∥BG,
∴∠AEF+∠EFB=180°,
∵∠EFB=32°,
∴∠AEF=148°,∴②正确;
∵根据折叠得出∠GEF=∠C′EF=32°=∠EFB,
∴∠BGE=32°+32°=64°,∴③正确;
∵∠EFB=32°,
∴∠EFD′=180°-32°=148°,
∵根据折叠得:∠EFD=∠EFD′=148°,
∴∠BFD=148°-32°=116°,∴④正确;
即正确的个数是4个,
故选D.
点评 本题考查了折叠的性质和平行线的性质等知识点,能灵活运用性质进行推理是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
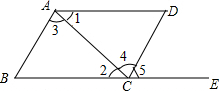 如图,下列能判断AB∥CD的条件有( )个
如图,下列能判断AB∥CD的条件有( )个| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
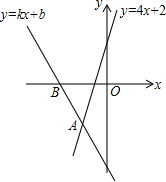 如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.
如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
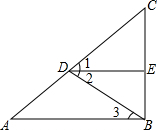 在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,
在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com