
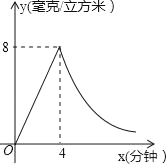
����Ŀ��Ϊ��Ԥ�������С���ijѧУ�Խ��Ҳ���ҩѬ��������������֪ҩ��ȼ��ʱ������ÿ���������еĺ�ҩ��y������/�����ף���ҩ���ȼ���ʱ��x�����ӣ�����������ҩ��ȼ����y��x�ɷ���������ͼ��ʾ������֪ҩ���ȼ��4����ȼ������ʱ����ÿ���������к�ҩ��Ϊ8���ˣ�
��1����ҩ��ȼ��ʱ��y��x֮�亯���ı���ʽ��
��2����ҩ��ȼ����y��x֮�亯���ı���ʽ��
��3���о���������������ÿ�����ĺ�ҩ��������2����ʱ��������Чɱ������еIJ�������ô�˴�������Чʱ���ж��
���𰸡���1��y=2x����2��y=![]() ����3���˴�������Чʱ��Ϊ16��1=15���ӣ�
����3���˴�������Чʱ��Ϊ16��1=15���ӣ�
��������
��1�����ô���ϵ�������ɵã�
��2�����ô���ϵ�������ɵã�
��3���������������ʽ��y=2ʱx��ֵ���Ӷ��ó��𰸣�
��1��ҩ��ȼ��ʱ����y=kx��
����4��8�����룬�ã�8=4k��
���k=2��
��y=2x��
��2��ҩ��ȼ������y=![]() ��
��
����4��8�����룬�ã�8=![]() ��
��
��ã�m=32��
��y=![]() ��
��
��3����y=2x�У���y=2ʱ��2x=2�����x=1��
��y=![]() �У���y=2ʱ��
�У���y=2ʱ��![]() =2�����x=16��
=2�����x=16��
��˴�������Чʱ��Ϊ16��1=15���ӣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ƽ��ֱ������ϵ�У����κ���y=��![]() x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
��1����գ�b=�� ����c=�� ����
��2���ڵ�P��Q�˶������У���APQ������ֱ������������˵�����ɣ�
��3����x���·����ö��κ�����ͼ�����Ƿ���ڵ�M��ʹ��PQM���Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ������ڣ�������˶�ʱ��t���������ڣ���˵�����ɣ�
��4����ͼ������N������Ϊ����![]() ��0�����߶�PQ���е�ΪH������NH������Q����ֱ��NH�ĶԳƵ�Q��ǡ�������߶�BC��ʱ����ֱ��д����Q������꣮
��0�����߶�PQ���е�ΪH������NH������Q����ֱ��NH�ĶԳƵ�Q��ǡ�������߶�BC��ʱ����ֱ��д����Q������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڽ�һԪ���η���ʱ������������һ�ֽⷨ���磺�ⷽ��x��x+4��=6��
�⣺ԭ���̿ɱ��Σ���[��x+2����2][��x+2��+2]=6����x+2��2��22=6����x+2��2=6+22����x+2��2=10��ֱ�ӿ�ƽ������������![]() ��
��![]() .���dz��������ֽⷨΪ��ƽ����������
.���dz��������ֽⷨΪ��ƽ����������
(1)��������������ƽ���������ⷽ�̣�x+2����x+6��=5ʱд�Ľ�����̣�
�⣺ԭ���̿ɱ��Σ���
[��x+��������][��x+����+��]=5��
��x+����2����2=5��
��x+����2=5+��2��
ֱ�ӿ�ƽ������������x1=����x2=�裮
���������е����������������������������衱��ʾ�����ֱ�Ϊ�� ������ ������ ������ ����
(2)������ƽ���������ⷽ�̣���x��3����x+1��=5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
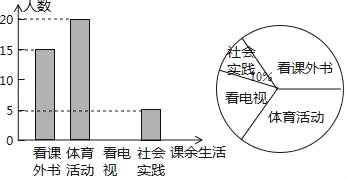
����Ŀ��Ϊ�˽�ij��ѧѧ�����������������ϲ���������顢������������ӡ����ʵ���ĸ�������������е���ͳ�ƣ��ִӸ�У�����ȡn��ѧ����Ϊ�����������ʾ�����ķ����ռ����ݣ������ʾ������ÿ��ѧ��ֻ��ѡ������һ��������ݵ���õ������ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ���ṩ����Ϣ������������⣺
��1����n��ֵ��
��2������Уѧ������1200�ˣ��Թ��Ƹ�Уϲ�������ӵ�ѧ��������
��3�������鵽ϲ���������4��ѧ������3��������1��Ů�����ִ���4��ѧ���������ȡ2��ѧ������ǡ�ó鵽2�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
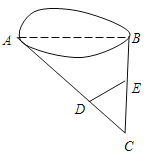
����Ŀ����ͼ����D��E�ֱ���AC��BC�ϣ�������CD��20m��CE��40m��AD=100m��BE=20m��DE=45m,��A��B���ؼ�ľ��롣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��DF��AD=BE��Ҫʹ��ABC�ա�DEF����������������ȷ���ǣ� ��
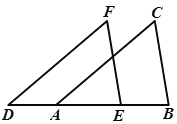
A.AC=DFB.BC��EFC.BC=EFD.��C=��F
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
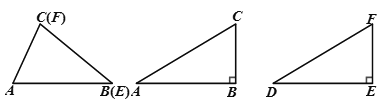
����Ŀ��ѧϰ��������ȫ�ȵ��ж���������SSS��SAS��ASA��AAS����ֱ��������ȫ�ȵ��ж���������HL�������Ǽ������������������������ߺ�����һ�ߵĶԽǶ�Ӧ����������ν����о���
������˼����
���Dz����������÷������Ա�ʾΪ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E��Ȼ��ԡ�B���з��࣬���Է�Ϊ����B��ֱ�ǡ��۽ǡ�����������������̽����
������̽����
��һ�����������BΪ���ʱ����ABC�͡�DEF��һ��ȫ�ȣ�
��1����ͼ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ������ó߹���ͼ��ȷ����D��ʹ��DEF�͡�ABC��ȫ�ȣ���д������������ͼ�ۼ�����
�ڶ������������BΪֱ��ʱ����ABC�ա�DEF��
��2����ͼ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E=90��������____������֪��Rt��ABC��Rt��DEF��
���������������BΪ�۽�ʱ����ABC�ա�DEF��
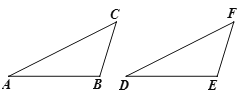
��3����ͼ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E���ҡ�B����E���Ƕ۽ǣ���֤����ABC�ա�DEF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��
��

��1�����![]() ��
��![]() �����ꣻ
�����ꣻ
��2����![]() ʱ��
ʱ��![]() ��ֵ����
��ֵ����![]() ʱ��
ʱ��![]() ��ֵ��
��ֵ��
��3������![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����ʹ
����ʹ![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ָо�,��Ӧû��ʲô�۵ı�,������Ȼ����,������״�ı���ȴ�ṩ���ڵij���Э���ϵ�һ�����еIJο�,����ѧ��,���������Ϊ�ƽ�ָ�.�������ɽŵ�������ij��������ߵı�����,����������Ļƽ�ָ��,Ҳ����˵,���˱�ֵԽ�ӽ�![]() ��Խ������һ�����ĸо�. ijŮʿ����Ϊ
��Խ������һ�����ĸо�. ijŮʿ����Ϊ![]() ,�ŵ�������ij��������ߵı�Ϊ
,�ŵ�������ij��������ߵı�Ϊ![]() Ϊ���������������ø߸�Ь�ﵽ��һЧ�� ,��ô��ѡ�ĸ߸�Ь�ĸ߶�ԼΪ�� ��
Ϊ���������������ø߸�Ь�ﵽ��һЧ�� ,��ô��ѡ�ĸ߸�Ь�ĸ߶�ԼΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com