
����Ŀ��Ϊ����ͬѧ���˽��Լ�������ˮƽ������1�����������ʦ��ȫ��45��ѧ��������һ������ģ����ԣ��÷־�Ϊ���������ɼ�����Ϊ10�֣�1�������ίԱ������β��Գɼ���������ͳ��ͼ�ͷ��������£�
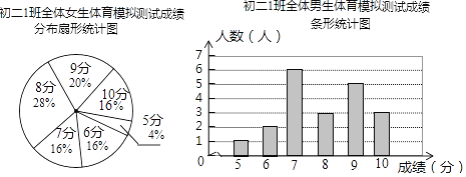
����1������ģ����Գɼ�������
ƽ���� | ���� | ��λ�� | ���� | |
���� | 2 | 8 | 7 | |
�� | 7.92 | 1.99 | 8 |
����������Ϣ������������⣺
��1������������________�ˣ�����Ů��________�ˣ�
��2����ȫ����1������ģ����Գɼ�������.
 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ���г���120��ˮ�����������̼ң����мס��ҡ������ֳ���ѡ��ÿ�����������������˷����±���ʾ��(����ÿ����������)
���� | �� | �� | �� |
����������(��/��) | 5 | 8 | 10 |
�����˷�(Ԫ/��) | 400 | 500 | 600 |
��1����ȫ��ˮ�����üס������ֳ��������ͣ����˷�8200Ԫ���ʷֱ���ס������ֳ���������
��2��Ϊ�˽�Լ�˷ѣ��г����Ե��üס��ҡ������ֳ��Ͳ������ͣ�ÿ�ֳ�������1��������֪���ǵ�������Ϊ16��������ͨ���з�����ķ����ֱ�������ֳ��͵�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ȫ��320��ѧ���ڵ�����ѵǰ����μ���һ��ˮƽ��ͬ�Ŀ��ԣ����ֶ���ͬһ�����ֳ������ϸ��������ϸ������������������ȼ���Ϊ���˽������ѵ��Ч�����ó�ǩ��ʽ�õ�����32��ѧ�������ο��Կ��ֵȼ��������Ƶ�ͳ��ͼ��ͼ��ʾ���Խ��ͼʾ��Ϣ�ش��������⣺

��1����32��ѧ����ѵǰ���ֵ���λ�����ڵĵȼ��� ����ѵ�ֵ���λ�����ڵĵȼ��� ��
��2����32��ѧ��������ѵ�����ֵȼ������ϸ��� �İٷֱ��� �½��� ��
��3�����Ƹ�У�������꼶�У���ѵ�ֵȼ�Ϊ���ϸ���������������ѧ������ ����
��4������Ϊ�������ƺ�����������ʲô��
�� �����ɣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
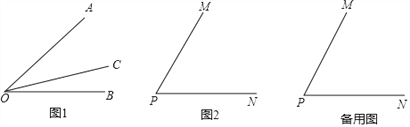
����Ŀ����̽����֪������ͼ1������OC�ڡ�AOB���ڲ���ͼ�й���3���ǣ���AOB����AOC�͡�BOC����������һ���ǵĶ�������һ���Ƕ������������������OC�ǡ�AOB�����ɷ�������
��1��һ���ǵ�ƽ������ ������ǵ����ɷ�����������������������������
��2����ͼ2������MPN=����������PQ�ǡ�MPN�����ɷ����������MPQ=�� �������ú����Ĵ���ʽ��ʾ�����п��ܵĽ����
�������о�������ͼ2������MPN=60����������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��10�����ٶ���ʱ����ת����PQ��PN��180��ʱֹͣ��ת����ת��ʱ��Ϊt�룮
��3����tΪ��ֵʱ������PM�ǡ�QPN�����ɷ�������
��4��������PMͬʱ�Ƶ�P��ÿ��5�����ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ�ǡ�MPN�����ɷ�����ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺������ȤС��ʱ����ʦ������������⣺
��ͼ1����ABC�У���AB=5��AC=3����BC���ϵ�����AD��ȡֵ��Χ��
С�������ھ��������������õ������µĽ���������ӳ�AD��E��ʹ��DE=AD��������BE������ACD�Ƶ�D��ʱ����ת180���õ���EBD������AB��AC��2AD��������ABE�У����������ε����߹�ϵ�ɵ�2��AE��8����1��AD��4��
������ʱ�����������������е��������������������Կ��ǹ������е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬһ���������У�
��1�����������ܵ���1��������������֤���������⣺��ͼ2������ABC�У�D��BC���ϵ��е㣬DE��DF��DE��AB�ڵ�E��DF��AC�ڵ�F������EF��
����֤��BE+CF��EF��������A=90����̽���߶�BE��CF��EF֮��ĵ�����ϵ��������֤����
��2��������չ����ͼ3����ƽ���ı���ABCD�У�AD=2AB��F��AD���е㣬��CE��AB������E���߶�AB�ϣ�����EF��CF����ô���н��ۢ١�DCF=![]() ��BCD����EF=CF����S��BEC=2S��CEF���ܡ�DFE=3��AEF����һ�������� ������ţ�.
��BCD����EF=CF����S��BEC=2S��CEF���ܡ�DFE=3��AEF����һ�������� ������ţ�.


ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1�����㣺��3���У�0�� ![]() +|3��
+|3�� ![]() |+��tan30�㣩��1
|+��tan30�㣩��1
��2�����������㣺��������ʵ��a��b������a��b=a��a��b��+1����ʽ�ұ���ͨ���ļӷ����������˷����㣮 ���磺2��5=2����2��5��+1
=2������3��+1
=��6+1
=��5
��3��x��ֵС��13����x��ȡֵ��Χ��������ͼ��ʾ�������ϱ�ʾ������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ķ�������������������ƽ�������нǵ�̽��Ƭ�Σ���������������.
̽��1����ͼl������ABC�У�O�ǡ�ABC���ACB��ƽ����BO��CO�Ľ��㣬ͨ���������֡�BOC=90![]() +
+![]() ��A,�������£�
��A,�������£�
��BO��CO�ֱ��ǡ�ABC�͡�ACB�Ľ�ƽ����
���1=![]() ��ABC, ��2=
��ABC, ��2=![]() ��ACB
��ACB
���l+��2=![]() (��ABC+��ACB)=
(��ABC+��ACB)= ![]() (180
(180![]() -��A)= 90
-��A)= 90![]() -
-![]() ��A
��A
���BOC=180![]() -(��1+��2) =180
-(��1+��2) =180![]() -(90
-(90![]() -
-![]() ��A)=90
��A)=90![]() +
+![]() ��A
��A
(1)̽��2����ͼ2�У�O��![]() ��ABC�����
��ABC�����![]() ��ACD��ƽ����BO��CO�Ľ��㣬�Է�����BOC���A�������Ĺ�ϵ����˵�����ɣ�
��ACD��ƽ����BO��CO�Ľ��㣬�Է�����BOC���A�������Ĺ�ϵ����˵�����ɣ�
(2)̽��3����ͼ3��, O����ǡ�DBC����ǡ�ECB��ƽ����BO��CO�Ľ��㣬���BOC���A�������Ĺ�ϵ����ֱ��д�����ۣ�
(3)��չ����ͼ4�����ı���ABCD�У�O�ǡ�ABC���DCB��ƽ����BO��CO�Ľ��㣬���BOC���A+��D�������Ĺ�ϵ����ֱ��д�����ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������õ������ϰ�ߣ���ѧ����ѧϰ������dz�����![]() ij��ѧΪ���˽����꼶ѧ��������������У���̴������꼶�����ȡ�˲���ѧ����������Щѧ��ͨ�������һ��������ʱ��
ij��ѧΪ���˽����꼶ѧ��������������У���̴������꼶�����ȡ�˲���ѧ����������Щѧ��ͨ�������һ��������ʱ��![]() ����
����![]() �����˵���
�����˵���![]() �ְѵ�������ΪA��B��C��D���飬���±���ʾ��ͬʱ�������������Ƴ�����������������ͳ��ͼ��
�ְѵ�������ΪA��B��C��D���飬���±���ʾ��ͬʱ�������������Ƴ�����������������ͳ��ͼ��

��� | �����ʱ�� |
A |
|
B |
|
C |
|
D |
|
����������ṩ����Ϣ������������⣺
![]() ����ͳ��ͼ��D�������ε�Բ�ĽǶ���Ϊ______��
����ͳ��ͼ��D�������ε�Բ�ĽǶ���Ϊ______��
![]() ��ȫƵ���ֲ�ֱ��ͼ��
��ȫƵ���ֲ�ֱ��ͼ��
![]() ��֪��У���꼶����1200��ѧ���������������꼶ѧ�����ж�����һ���������ʱ�䲻����20���ӣ�
��֪��У���꼶����1200��ѧ���������������꼶ѧ�����ж�����һ���������ʱ�䲻����20���ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е�ʽ������a=b����5��2a=5��2b������a=b����ac=bc������a=b����![]() ������
������![]() ����3a=2b��
����3a=2b��
����a2=b2����a=b��������ȷ����_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com