
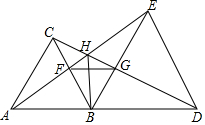
 如图,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60°.⑤△BFG是等边三角形,其中正确的有①②④⑤.
如图,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60°.⑤△BFG是等边三角形,其中正确的有①②④⑤. 分析 由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
解答 解:∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD,故①正确
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE,
∴BG=BF,∠BFG=∠BGF=60°,故②正确,
∴△BFG是等边三角形,故⑤正确,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,故④正确,
∵∠FGB=∠GBD=60°,
∴FG∥AD,
不妨设FG⊥BH,则BH⊥AD,易证△ABH≌△DBH,可得AB=BD,显然与已知条件矛盾,故③错误,
故答案为①②④⑤.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a>3b | B. | a-3>b-3 | C. | -3a>-3b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com