
【题目】如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.
(1)在图1中画出一条长为![]() 的线段MN(M,N分别为格点)
的线段MN(M,N分别为格点)
(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;
(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.

科目:初中数学 来源: 题型:
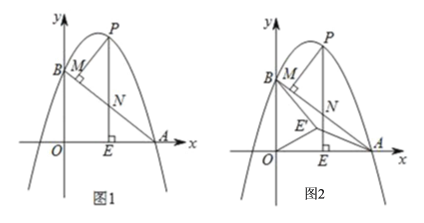
【题目】如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
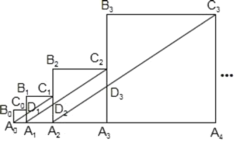
【题目】如图,正方形A0B0C0A1的边长为1,正方形A1B1C1A2的边长为2,正方形A2B2C2A3的边长为4,正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBnnAn+1,且点A0,A1,A2,A3,…,An+1在同一条直线上,连接A0C1交A1B1于点D1,连接A1C2交A2B2于点D2,连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1,四边形A1B1C1D2的面积为S2,四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn,则S2019=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
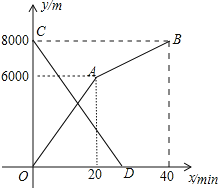
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开口向下的抛物线y=a(x+1)(x﹣4)与x轴的交点为A、B(A在B的左边),与y轴交于点C.连接AC、BC.
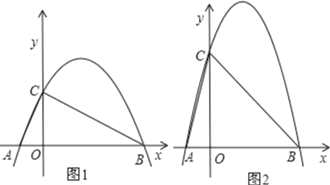
(1)若△ABC是直角三角形(图1),求二次函数的解析式;
(2)在(1)的条件下,将抛物线沿y轴的负半轴向下平移k(k>0)个单位,使平移后的抛物线与坐标轴只有两个交点,求k的值;
(3)当点C坐标为(0,4)时(图2),P、Q两点同时从C点出发,点P沿折线COB运动到点B,点Q沿抛物线(在第一象限的部分)运动到点B,若P、Q两点的运动速度相同,请问谁先到达点B?请说明理由.(参考数据:![]() .6,
.6,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
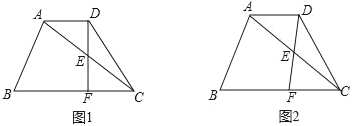
【题目】已知在梯形ABCD中,AD∥BC,AC=BC=10,cos∠ACB=![]() ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
(1)如图1,当DF⊥BC时,求AD的长;
(2)设EC=y,求y关于x的函数解析式,并直接写出定义域;
(3)当△DFC是等腰三角形时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
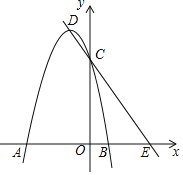
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.
(1)当a=﹣1时,求抛物线顶点D的坐标,OE等于多少;
(2)OE的长是否与a值有关,说明你的理由;
(3)设∠DEO=β,45°≤β≤60°,求a的取值范围;
(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m的函数解析式及自变量m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
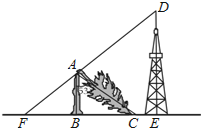
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com