
【题目】如图,等腰三角形纸片ABC中,AD⊥BC与点D,BC=2,AD=![]() ,沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形中较长对角线的长为__________.
,沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形中较长对角线的长为__________.

【答案】2或![]() 或
或![]()
【解析】
分别以AC,AD, BD为对角线拼成平行四边形,然后利用勾股定理求解
解:由题意可知,等腰△ABC中,AD⊥BC
∴BD=CD=![]() ,AC=
,AC=![]()
①当以AC边为对角线时,此时平行四边形ADCB为矩形,两对角线长度相等为2;
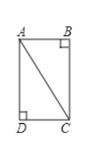
②当以AD边为对角线时,此时平行四边形BDCA的较长对角线是BC,
过点B作BE⊥CD,交CD的延长线于点E
此时四边形BEDA为矩形
∴BE=AD=![]() ,DE=AB=1,EC=DE+CD=2
,DE=AB=1,EC=DE+CD=2
∴在Rt△BEC中,![]()
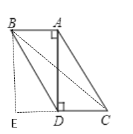
③当以BD为对角线时,此时平行四边形ADCB的较长对角线是AC
过点C作CE⊥AD,交AD的延长线于点E
此时四边形DECB是矩形
∴DE=BC=AD=![]() ,CE=BD=1,AE=AD+DE=
,CE=BD=1,AE=AD+DE=![]()
∴在Rt△AEC中,AC=![]()

综上,平行四边形中较长对角线的长为2或![]() 或
或![]()
故答案为:2或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级 | 做家务时间(小时) | 频数 | 百分比 |
A | 0.5≤x<1 | 3 | 6% |
B | 1<x<1.5 | a | 30% |
C | 1.5≤x<2 | 20 | 40% |
D | 2≤x<2.5 | b | m |
E | 2.5≤x<3 | 2 | 4% |
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示则这20户家庭该月用电量的众数和中位数、平均数分别是( )

A. 180,160,164B. 160,180;164C. 160,160,164D. 180,180,164
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则![]() 的最大值是( )
的最大值是( )

A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
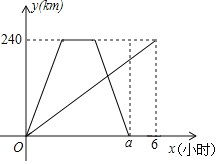
【题目】A、B两地相距240km,甲骑摩托车由A地驶往B地,乙驾驶汽车由B地驶往A地,甲乙两人同时出发,乙达到A地停留1小时后,按原路原速返回B地,甲比乙晚1小时到达B地,甲、乙两人行驶过程中均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.
(1)在上述变化过程中,自变量是______,因变量是______;
(2)a的值为______;
(3)甲到达B地共需______小时;甲骑摩托车的速度是______km/h;
(4)乙驾驶汽车的速度是多少km/h?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠BAC=90°,∠BAC和∠ABC的平分线交于点P
(1)如图1,在BC上取一点D,使得DB=AB,连接PD,△ABP与△DBP全等吗?为什么?
(2)在(1)的条件下,若DP=DC,则BC=AB+AP是否成立?请说明理由;
(3)如图2,在AC上取一点E,使得AE=AB,连接PE、PC,若∠ABC=60°,求∠EPC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
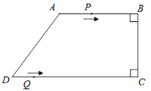
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠BCD=90°,AD=10cm,BC=8cm,CD=16cm.点P从点A出发,以每秒3cm的速度沿折线段AB—BC—CD运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,设运动时间为t秒(![]() ).
).
(1)求AB的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P运动过程中,当![]() 秒的时候,使得△BPD的面积为20cm2.
秒的时候,使得△BPD的面积为20cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王的房子准备开始装修,请来师徒二人做泥水.已知师傅单独完成需10天,徒弟单独完成需15天。
(1)若两人先合作2天,剩下的由徒弟单独做,结果超出老王预期的工期3天完成,求老王预期的工期天数;
(2)若师傅的工价每天300元,徒弟的工价每天220元,老王房子的泥水工价预算不超过3180元,问师傅至少要做几天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com