
【题目】如图,在平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,m),B(n,3)两点,一次函数
的图象交于A(1,m),B(n,3)两点,一次函数![]() 的图象与y轴交于点C.
的图象与y轴交于点C.
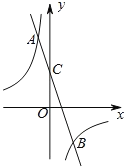
(1)求一次函数的解析式;
(2)点P是x轴上一点,且△BOP的面积是△BOC面积的2倍,求点P的坐标.
【答案】(1)y=3x+3;(2)(4,0)或(4,0).
【解析】
(1)把点A(-1,m),B(n,-3)代入![]() 求得A(-1,6),B(2,-3),由于一次函数y=kx+b的图象过A(-1,6),B(2,-3)两点,解方程组,即可得到结果;
求得A(-1,6),B(2,-3),由于一次函数y=kx+b的图象过A(-1,6),B(2,-3)两点,解方程组,即可得到结果;
(2)由于一次函数y=-3x+3与y轴交点C(0,3)且B(2,-3)求得△BOC面积=3,由于P是x轴上一点,且△BOP的面积是△BOC面积的2倍,设P(a,0),得到方程![]() ×|a|×2=6,解得即可得到结果.
×|a|×2=6,解得即可得到结果.
(1)∵点A(1,m),B(n,3)在反比例函数![]() 的图象上,
的图象上,
∴m=![]() =6,3=
=6,3=![]() ,
,
∴n=2.
∴A(1,6),B(2,3),
∵一次函数y=kx+b的图象过A(1,6),B(2,3)两点,
∴![]() ,解方程组得
,解方程组得![]() ,
,
∴一次函数的解析式为y=3x+3;
(2)∵一次函数y=3x+3与y轴交点C(0,3),且B(2,3)
∴△BOC面积=3,
∵P是x轴上一点,且△BOP的面积是△BOC面积的2倍,
∴设P(a,0),
∴![]() ×|a|×3=6,解得,a=±4.
×|a|×3=6,解得,a=±4.
∴点P的坐标为(4,0)或(4,0).


科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为( )
A.y=1.5x+3B.y=1.5x-3C.y=-1.5x+3D.y=-1.5x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
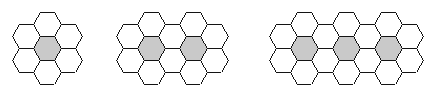
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:
![]()
![]()
![]()
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
查看答案和解析>>
科目:初中数学 来源: 题型:
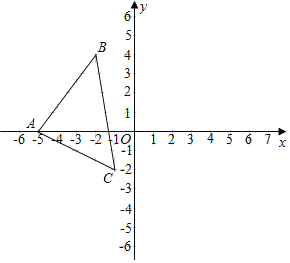
【题目】△ABC三顶点A(﹣5,0)、B(﹣2,4)、C(﹣1,﹣2),△A'B'C'与△ABC关于y轴对称.
(1)直接写出A'、B'、C'的坐标;
(2)画出△A'B'C';
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() (x>0)的图象上,点D的坐标为(4,3).设AB所在的直线解析式为
(x>0)的图象上,点D的坐标为(4,3).设AB所在的直线解析式为![]() ,若将菱形ABCD沿x轴正方向平移m个单位,
,若将菱形ABCD沿x轴正方向平移m个单位,
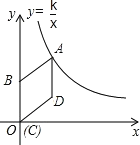
①当菱形的顶点B落在反比例函数的图象上,求m的值;
②在平移中,若反比例函数图象与菱形的边AD始终有交点,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
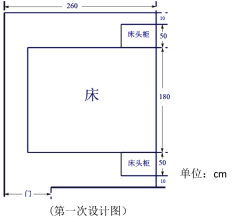
【题目】小丽家在装修,虽然房间比较小,但是小丽总想睡1.8米宽的大床,那样抱着她的大娃娃睡多好啊,妈妈说:“你已经八年级了,自己设计一下,怎样可以把1.8米宽的床放好,并且还比较美观?”下面是小丽的第一次设计图:1.8米宽的床一般长2.2米,床头柜一般需要50cm,门宽80cm,只能往房里开。
妈妈看了设计图以后,怀疑地说:“像你这样设计,门好像打不开啊。”请通过计算说明,此时门能否完全打开?
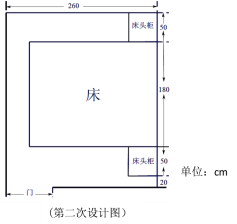
小丽考虑将家具整体平移一下,她又设计了第二种方案,这时妈妈看了一会,问小丽:“你确定门能完全打开?”,小丽得意地笑了,请通过计算说明为什么这次可以了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(﹣1,n)和Q(3,n)都在二次函数y=x2+bx﹣1的图象上.
(1)求b、n的值;
(2)将二次函数图象向上平移几个单位后,得到的图象与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
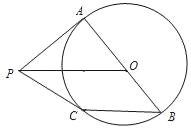
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com