
���꼶��ѧѧϰ����С����ѧ����ͼ�ε����ơ���һ�º��ֿɽ����������εĶ��塢�ж��Լ�������չ�����Ρ����ε�������ȥ���磺���ǿ��Զ��壺�����Ϳ�֮����ȵľ��������ƾ��Σ������ƾ���Ҳ�����µ����ʣ����ƾ��εĶԽ���֮�ȵ������Ʊȣ��ܳ��ȵ������Ʊȣ�����ȵ������Ʊȵ�ƽ���ȵȣ�����������ѧϰС�飬һͬ̽���������⣺

��1��д���ж��������Ƶ�һ���ж�����������һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ����������������������ƣ�
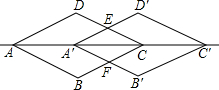
��2����ͼ��������ABCD����ֱ��AC����ƽ�ƺ�õ�����A��B��C��D�䣬��֤�����ı���A��FCE�����Σ�������ABCD������A��FCE��
��3����AC=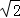 ������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
��������
������������ƶ���ε�����ıȵ������Ʊȵ�ƽ���������֪����ıȣ��Ϳ�������߳��ıȣ����A��C�ij��Ϳ��Խ����
�⣺��1����һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ���������3�֣�
��2������AD��A��E��AB��A��F���á�DAB=��D��A��B��
�����ã�1���Ľ��ۣ��õ�֤������6�֣�
��3��������ABCD������A��FCE������A��FCE�����������ABCD�����һ�룬
������ABCD������A��FCE�������Ϊ2��1��
���Ӧ��֮��Ϊ ��1����AC��A��C=
��1����AC��A��C= ��1����7�֣�
��1����7�֣�
��AC= ��
��
��A��C=1����9�֣�
��AA��= ��1����10�֣�
��1����10�֣�
���㣺���ƶ���ε����ʣ�ƽ�Ƶ����ʣ�
������


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�������ѧ��Ԫ���Ų��Ծ�-���ƶ���ε����ʣ��������� ���ͣ������
���꼶��ѧѧϰ����С����ѧ����ͼ�ε����ơ���һ�º��ֿɽ����������εĶ��塢�ж��Լ�������չ�����Ρ����ε�������ȥ���磺���ǿ��Զ��壺�����Ϳ�֮����ȵľ��������ƾ��Σ������ƾ���Ҳ�����µ����ʣ����ƾ��εĶԽ���֮�ȵ������Ʊȣ��ܳ��ȵ������Ʊȣ�����ȵ������Ʊȵ�ƽ���ȵȣ�����������ѧϰС�飬һͬ̽���������⣺
��1��д���ж��������Ƶ�һ���ж�����������һ��Ƕ�Ӧ��ȣ�������Խ��߶�Ӧ�ɱ����������������������ƣ�
��2����ͼ��������ABCD����ֱ��AC����ƽ�ƺ�õ�����A��B��C��D�䣬��֤�����ı���A��FCE�����Σ�������ABCD������A��FCE��
��3����AC= ������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2009�꽭��ʡ�����л��������ģ�⿼����ѧ�Ծ��������棩 ���ͣ������
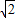 ������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com