
【题目】如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了相同的方法进行解决:将△ABD沿AD所在的直线对折得到△ADF(如图2);请证明小敏的发现的是正确的.

【答案】见解析
【解析】试题分析:(1)如图1,根据图形、已知条件推知∠BAD+∠MAE=∠DAM+∠EAC=45°,所以∠MAE=∠EAC,即AE平分∠MAC;(2)小颖的方法是应用折叠对称的性质和SAS得到△AEF≌△AEC,在Rt△OCE中应用勾股定理而证明;小亮的方法是将△ABD绕点A逆时针旋转90°得到△ACG,根据旋转的性质用SAS得到△ACE≌△ACG,从而在Rt△CEG中应用勾股定理而证明.
试题解析:1)证明:如图1,∵∠BAC=90°,
∴∠BAD+∠DAM+∠MAE+∠EAC=90°.
∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∵∠BAD=∠DAM,
∴∠BAD+∠EAC=∠DAM+∠EAC=45°,
∴∠BAD+∠MAE=∠DAM+∠EAC,
∴∠MAE=∠EAC,即AE平分∠MAC;
(2)如图2,连接EF.

由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
∴由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,
∵ AF=AC,∠FAE=∠CAE,AE=AE ,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2. (利用旋转的方法证明相应给分)


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
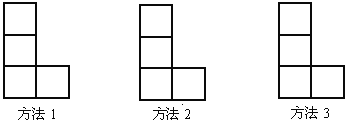
【题目】① 如图,由小正方形组成的L形图中,用三种方法分别在图中添一个小正方形使图形成为轴对称图形:
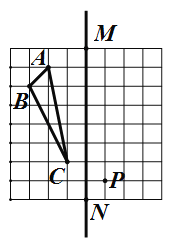
② 如图,在正方形网格上的一个△ABC.
⑴ 作△ABC关于直线MN的对称图形(不写作法);
⑵ 以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出 个三角形与△ABC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
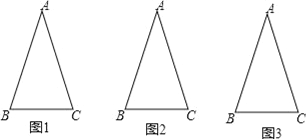
【题目】如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)
(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是 度和 度;
(2)在图2中画2条线段,使图中有4个等腰三角形;
(3)继续按以上操作发现:在△ABC中画n条线段,则图中有 个等腰三角形,其中有 个黄金等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
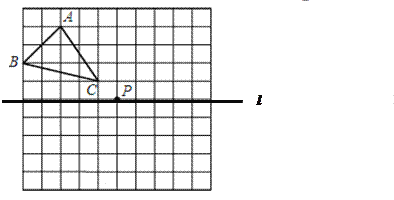
【题目】如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线l的对称的△A1B1C1.
(2)画出△ABC关于点P的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形_______________(是或否)轴对称图形,如果是轴对称图形,请画出对称轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com