
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDGF周长的最小值为![]() ,其中,判断正确的序号是( )
,其中,判断正确的序号是( )

A.①②B.②③C.①③D.②③④
【答案】B
【解析】
根据抛物线在x轴上方所对应的自变量的范围可判断①;先求出抛物线的对称轴,利用抛物线的对称性求出b可判断②;先求出抛物线的对称轴,然后比较点P和Q到对称轴距离的大小,然后可以确定函数值的大小,即可判断③;先求出D、E两点的坐标,然后求出符合题意的对称点坐标分别为(-1,4)(2,-3),然后根据勾股定理计算即可判断④.
①当x>0时,y不一定大于0,故错误;
②对称轴为1,当a=-1,b=3,故正确;
③![]() >1,∴
>1,∴![]()
Q点距离对称轴较远,∴y1>y2,故正确;
④m=2时,D(1,4),E(2,3),
可得出DE的对称点为(-1,4)(2,-3),
四边形DEFG的周长为![]() ,故错误;
,故错误;
故答案为:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(猜想) 如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG.试猜想线段BG和AE的数量关系是 ;
(探究) 如图2,正方形DEFG绕点D逆时针旋转α(0°<α<360°).试判断你猜想的结论是否仍然成立,请利用图2证明你的结论;
(应用) 在图2中,BC=DE=4.当AE取最大值时,AF的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
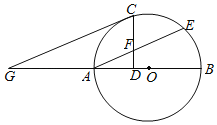
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若sinG=0.6,CF=4,求GA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E点.

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,高AD=8,M、N、P分别在边AB、BC、AC上移动,但不与A、B、C重合,连接MN、NP、MP,且MP始终与BC保持平行,AD与MP相交于点E,设MP=x,△MNP的面积用y表示.
(1)求y关于x的函数关系式;
(2)当x取什么值时,y有最大值,并求出的最大值;
(3)当x取什么值时,△MNP是等腰直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
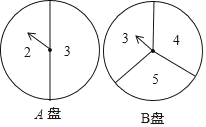
【题目】甲、乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两同学分别同时转动两个转盘各1次,当转盘停止后,指针所在区域的数字之积为偶数时甲胜;数字之积为奇数时乙胜.若指针恰好在分割线上,则需要重新转动转盘.
(1)用树状图或列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
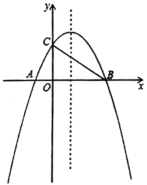
(1)求该抛物线的函数表达式;
(2)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)点![]() 是直线
是直线![]() 上方抛物线上的点,若
上方抛物线上的点,若![]() ,求出
,求出![]() 点的到
点的到![]() 轴的距离.
轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
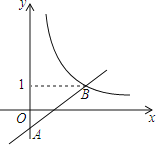
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com