
科目:初中数学 来源: 题型:选择题
| A. | 随机抽取100位女性老人 | |
| B. | 随机抽取100位男性老人 | |
| C. | 随机抽取公园内100位老人 | |
| D. | 在城市和乡镇各选10个点,每个点任选5位老人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)
如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
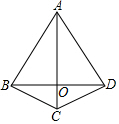 如图,四边形ABCD中,AB=AD,∠ABC=∠ADC.
如图,四边形ABCD中,AB=AD,∠ABC=∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
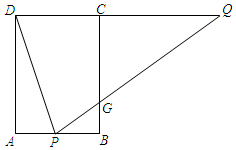 如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com