
分析 (1)根据两个不同的取值范围,利用销售利润=销售量×每一件的销售利润列出函数即可;
(2)利用(2)中的函数解析式,结核函数的性质求得最大值,比较得出答案即可.
解答 解:(1)①当1≤x≤9时,
w=(y-20)p=($\frac{1}{2}$x+30-20)(30-x)=-$\frac{1}{2}$x2+5x+300;
②当10≤x≤18时,
w=(y-20)p=($\frac{150}{x}$+20-20)(30-x)=$\frac{4500}{x}$-150;
(2)当1≤x≤9时,
w=-$\frac{1}{2}$x2+5x+300=-$\frac{1}{2}$(x-5)2+312.5,
∵-$\frac{1}{2}$<0,
∴当x=5时,w有最大值为312.5;
当10≤x≤18时,
w=$\frac{4500}{x}$-150;
∵4500>0,
∴w随着x的增大而减小,
∴当x=10时,w=$\frac{4500}{x}$-150有最大值$\frac{4500}{10}$-150=300,
∵312.5>300,
∴该网店在试营销期间,第5天获得的利润最大,最大利润是312.5元.
点评 此题考查二次函数与反比例函数的实际运用,注意函数的取值范围是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.
已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x2+3 | B. | y=2x2+1 | C. | y=2(x+1)2+2 | D. | y=2(x-1)2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
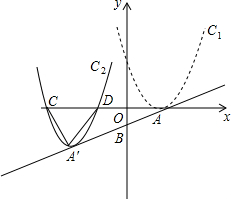 如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )
如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com