
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
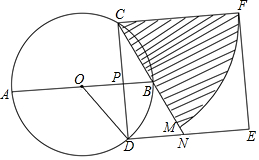 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
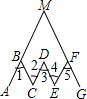 完成推理填空
完成推理填空查看答案和解析>>
科目:初中数学 来源: 题型:选择题
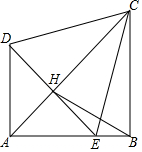 将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:| A. | 只有①② | B. | 只有③④ | C. | 只有①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
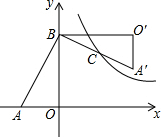 如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com