
【题目】如图,在平面直角坐标系xOy,已知二次函数y=﹣![]() x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
(1)求二次函数的表达式;
(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;
(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF与△DEF全等,求点E的坐标.

【答案】(1)二次函数的表达式为y=﹣![]() x2+2x;(2)BQ=
x2+2x;(2)BQ=![]() ;(3)点E的坐标为:(
;(3)点E的坐标为:(![]() ,0)或(
,0)或(![]() ,
,![]() )或(2+
)或(2+![]() ,2﹣
,2﹣![]() )或(4,0).
)或(4,0).
【解析】
试题(1)利用待定系数法求二次函数的表达式;
(2)先求出OB和AB的长,根据勾股定理的逆定理证明∠ABO=90°,由对称计算∠QCB=60°,利用特殊的三角函数列式可得BQ的长;
(3)因为D在OB上,所以F分两种情况:
i)当F在边OA上时,ii)当点F在AB上时,
当F在边OA上时,分三种情况:
①如图2,过D作DF⊥x轴,垂足为F,则E、F在OA上,②如图3,作辅助线,构建△OFD≌△EDF≌△FGE,③如图4,将△DOF沿边DF翻折,使得O恰好落在AB边上,记为点E;当点F在OB上时,过D作DF∥x轴,交AB于F,连接OF与DA,依次求出点E的坐标即可.
试题解析:(1)将点A的坐标代入二次函数的解析式得:﹣![]() ×42+4b=0,解得b=2,
×42+4b=0,解得b=2,
∴二次函数的表达式为y=﹣![]() x2+2x.
x2+2x.
(2)∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣2)2+2,
(x﹣2)2+2,
∴B(2,2),抛物线的对称轴为x=2.
如图1所示:
由两点间的距离公式得:OB=![]() =2
=2![]() ,BA=
,BA=![]() =2
=2![]() .
.
∵C是OB的中点,
∴OC=BC=![]() .
.
∵△OB′C为等边三角形,
∴∠OCB′=60°.
又∵点B与点B′关于CQ对称,
∴∠B′CQ=∠BCQ=60°.
∵OA=4,OB=2![]() ,AB=2
,AB=2![]() ,
,
∴OB2+AB2=OA2,
∴∠OBA=90°.
在Rt△CBQ中,∠CBQ=90°,∠BCQ=60°,BC=![]() ,
,
∴tan60°=![]() ,
,
∴BQ=![]() CB=
CB=![]() ×
×![]() =
=![]() .
.
(3)分两种情况:
i)当F在边OA上时,
①如图2,过D作DF⊥x轴,垂足为F,
∵△DOF≌△DEF,且E在线段OA上,
∴OF=FE,
由(2)得:OB=2![]() ,
,
∵点D在线段BO上,OD=2DB,
∴OD=![]() OB=
OB=![]() ,
,
∵∠BOA=45°,
∴cos45°=![]() ,
,
∴OF=ODcos45°=![]() =
=![]() ,
,
则OE=2OF=![]() ,
,
∴点E的坐标为(![]() ,0);
,0);
②如图3,过D作DF⊥x轴于F,过D作DE∥x轴,交AB于E,连接EF,过E作EG⊥x轴于G,
∴△BDE∽△BOA,
∴![]() =
=![]() ,
,
∵OA=4,
∴DE=![]() ,
,
∵DE∥OA,
∴∠OFD=∠FDE=90°,
∵DE=OF=![]() ,DF=DF,
,DF=DF,
∴△OFD≌△EDF,
同理可得:△EDF≌△FGE,
∴△OFD≌△EDF≌△FGE,
∴OG=OF+FG=OF+DE=![]() +
+![]() =
=![]() ,EG=DF=ODsin45°=
,EG=DF=ODsin45°=![]() ,
,
∴E的坐标为(![]() ,
,![]() );
);
③如图4,将△DOF沿边DF翻折,使得O恰好落在AB边上,记为点E,
过B作BM⊥x轴于M,过E作EN⊥BM于N,
由翻折的性质得:△DOF≌△DEF,
∴OD=DE=![]() ,
,
∵BD=![]() OD=
OD=![]() ,
,
∴在Rt△DBE中,由勾股定理得:BE=![]() =
=![]() ,
,
则BN=NE=BEcos45°=![]() ×
×![]() =
=![]() ,
,
OM+NE=2+![]() ,BM﹣BN=2﹣
,BM﹣BN=2﹣![]() ,
,
∴点E的坐标为:(2+![]() ,2﹣
,2﹣![]() );
);
ii)当点F在AB上时,
过D作DF∥x轴,交AB于F,连接OF与DA,
∵DF∥x轴,
∴△BDF∽△BOA,
∴![]() ,
,
由抛物线的对称性得:OB=BA,
∴BD=BF,
则∠BDF=∠BFD,∠ODF=∠AFD,
∴OD=OB﹣BD=BA﹣BF=AF,
则△DOF≌△DAF,
∴E和A重合,则点E的坐标为(4,0);
综上所述,点E的坐标为:(![]() ,0)或(
,0)或(![]() ,
,![]() )或(2+
)或(2+![]() ,2﹣
,2﹣![]() )或(4,0).
)或(4,0).







 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
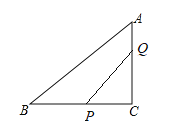
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 移动,同时动点
移动,同时动点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 移动,设它们的运动时间为
移动,设它们的运动时间为![]() .
.
(1)![]() 为何值时,
为何值时,![]() 的面积等于
的面积等于![]() 面积的
面积的![]() ;
;
(2)运动几秒时,![]() 与
与![]() 相似?
相似?
(3)在运动过程中,![]() 的长度能否为
的长度能否为![]() ?试说明理由
?试说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图
任务一:下面是小希设计的“过直线外一点作已知直线的平行线”的尺规作图过程.

已知:直线l及直线外一点P.
求作:直线PQ,使得PQ∥l.
作法:如图
①在直线l上取一点O,连接OP,以点O为圆心,OP为半径画圆,交直线l与点A和点B;②连接AP,以点B为圆心,AP长为半径在直线l上方画弧交⊙O于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小希设计的尺规作图步骤完成下列问题:
(1)在图1中使用直尺和圆规,补全图形;(保留作图痕迹)
(2)证明:PQ∥l
任务二:已知:直线l及直线l外一点M.
请根据下列提供的数学原理,选择其一,在图2中使用直尺和圆规作直线MN,使得MN∥l.(保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com