
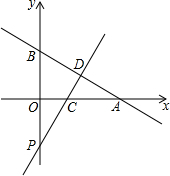
 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.分析 (1)首先求出A、B两点的坐标各是多少;然后将△AOB沿直线CD折起,点A与点B重合,可得CD垂直平分AB,据此求出点D的坐标以及CD所在的直线的斜率,进而求出CD所在的直线的解析式以及点C的坐标即可.
(2)首先求出AC=4,再根据点P是射线DC上的一点,设点P的坐标是(x,$\sqrt{3}x-2\sqrt{3}$)(x<3),然后根据PC=AC=4,列出方程,求出x的值是多少,进而求出点P的坐标即可.
解答 解:(1)∵一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,
∴A(6,0)、B(0,2$\sqrt{3}$),
∵将△AOB沿直线CD折起,点A与点B重合,
∴CD垂直平分AB,
∴点D的坐标是(3,$\sqrt{3}$),
∴CD所在的直线的斜率是:$\frac{-1}{-\frac{\sqrt{3}}{3}}=\sqrt{3}$,
∴CD所在的直线的解析式是:y=$\sqrt{3}$(x-3)$+\sqrt{3}$=$\sqrt{3}x-2\sqrt{3}$,
∴点C的坐标是(2,0).
(2)∵A(6,0)、C(2,0),
∴AC=6-2=4,
∵点P是射线DC上的一点,
∴设点P的坐标是(x,$\sqrt{3}x-2\sqrt{3}$)(x<3),
∵PC=AC=4,
∴(x-2)2+${(\sqrt{3}x-2\sqrt{3})}^{2}$=42=16,
整理,可得x2-4x=0,
解得x=0或x=4,
∵x<3,
∴x=4不符合题意,
∴点P的坐标是(0,-2$\sqrt{3}$).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了直线解析式的求法,以及一元二次方程的解法,要熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.1010010001 | B. | $\sqrt{9}$ | C. | $\root{3}{-64}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -4 | C. | -$\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com