
���� ���ȼ��㣬Ȼ���ٱȽϴ�С��
�ڿɷ�Ϊa��bͬ�ţ�a����ţ�a��b����һ����Ϊ0�������������
�۸��ݣ�2���еĽ��ۼ��ɵó��𰸣�
��� �⣺��|2|+|6|=2+6=8��|2-6|=|-4|=4��
��|2|+|6|��|2-6|��
|-2|+|3|=2+3=5��|��-2��-3|=|-5|=5
��|-2|+|3|=|��-2��-3|��
|3|+|-5|=3+5=8��|3-��-5��|=|8|=8��
��|3|+|-5|=|3-��-5��|��
|-$\frac{1}{2}$|+|-$\frac{1}{3}$|=$\frac{1}{2}+\frac{1}{3}$=$\frac{5}{6}$��|��-$\frac{1}{2}$��-��-$\frac{1}{3}$��|=|$-\frac{1}{6}$|=$\frac{1}{6}$
��|-$\frac{1}{2}$|+|-$\frac{1}{3}$|��|��-$\frac{1}{2}$��-��-$\frac{1}{3}$��|��
|0|+|-5|=0+5=5��|0-��-5��|=5��
��|0|+|-5|=|0-��-5��|��
�ʴ�Ϊ������=��=������=��
���ɣ�1����֪����a��bͬ��ʱ��|a|+|b|��|a-b|��
��a��b���ʱ��|a|+|b|=|a-b|��
��a��b����һ��Ϊ0ʱ��|a|+|b|=|a-b|��
�ۡ�|x|+2=|x-2|���ɣ�2����֪x��0��
���� ������Ҫ������Ǿ���ֵ�ļ��㣬���ݼ����ҳ����еĹ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5\sqrt{2}}{3}$ | B�� | $��\frac{5\sqrt{2}}{3}$ | C�� | $\frac{50}{9}$ | D�� | $��\frac{50}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
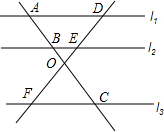 ��֪��l1��l2��l3��
��֪��l1��l2��l3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�BEƽ�֡�ABC��AD�ڵ�E��DFƽ�֡�ADC��BC�ڵ�F��
��ͼ����?ABCD�У�BEƽ�֡�ABC��AD�ڵ�E��DFƽ�֡�ADC��BC�ڵ�F���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com